Cálculo Diferencial del Semestre 2021A página de Tareas Avisos, Apuntes y Material de Apoyo para las clases por Meet.
Índice del Contenido
Temario
Tareas
En esta sección se publicarán las tareas para entregar en el Semestre
Avisos
Calendario del Semestre con las fechas importantes!!
Apunte De Funciones Y Relaciones
Relación es una regla de correspondencia entre los elementos de dos conjuntos sin ninguna restricción


Esta relación se representa con el siguiente conjunto de pares ordenados:
R={(x_{1},y_1 ),(x_{1},y_{2} ),(x_{2},y_{1} ),(x_{2},y_{2} ),(x_{3},y_{3} ),(x_{4},y_{4} )}
Función:
El concepto de función es uno de los más importantes en las matemáticas. Las funciones no sólo representan fórmulas, o lugares geométricos, también se utilizan como modelos matemáticos o planteamientos que resuelven problemas de la vida real.
A continuación se dan algunas definiciones de función:
- Es una regla de correspondencia que asocia a los elementos de dos conjuntos. La cual a cada elemento del primer conjunto (dominio) le asocia un solo elemento del segundo conjunto (contradominio).
- Sean A y B dos conjuntos y f una regla que a cada x ∈ A asigna un único elemento f (x) del conjunto B, se dice que f es una función que va del conjunto A al B, y se representa de la siguiente forma: f: A → B, donde al conjunto A se le llama dominio y al B contradominio, que también se representa por medio de un diagrama de flechas:


Una función es una colección de pares ordenados con la siguiente propiedad: Si (a, b) y (a, c) pertenecen a una colección, entonces se cumple que b = c; es decir, en una función no puede haber dos pares con el mismo primer elemento.
1.- Determina si los siguientes diagramas representan una función o una relación:
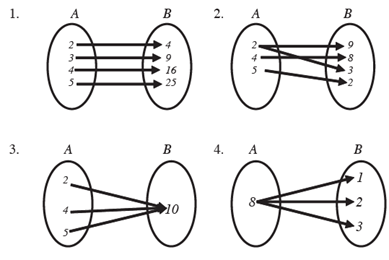

Solución:
El primer y el tercer diagramas corresponden a una función ya que a cada elemento del conjunto A se le asigna un solo elemento del conjunto B.
En el segundo diagrama al menos a un elemento del conjunto A se le asignan dos elementos del conjunto B, mientras que en el cuarto diagrama el elemento 8 se asocia con tres elementos del conjunto B, por tanto, se concluye que estos conjuntos representan una relación.
2.- Determina si los siguientes conjuntos de pares ordenados corresponden a una función o a una relación:
A= {(-2,4),(3,9),(4,16),(5,25)}
B= {(3,2),(3,6),(5,7),(5,8)}
C= {(2,4),(3,4),(5,4),(6,4)}
A= {(2,4),(6,2),(7,3),(4,12),(2,6)}
Solución:
Los conjuntos A y C son funciones ya que el primer elemento de cada par ordenado no se repite. En el conjunto B el 3 y el 5 aparecen dos veces como primer elemento del par ordenado mientras que en el conjunto M al 2 se le están asignando el 4 y el 6 como segundo elemento, por tanto, B y M son relaciones.
Las funciones y relaciones pueden tener una representación gráfica en el plano cartesiano. Para distinguir si se trata de una función o una relación basta con trazar una recta paralela al eje “Y” sobre la gráfica; si ésta interseca en dos o más puntos es una relación, si sólo interseca un punto será una función.
3.- Determina si las siguientes gráficas representan una relación o una función.
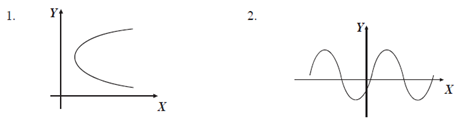
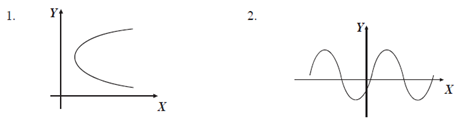
Solución:
Se traza una recta vertical en ambas gráficas y se observa que en la primera intersecta en dos puntos a la gráfica, por tanto, representa una relación y en la segunda, la recta vertical interseca en un punto a la gráfica, por consiguiente representa una función.
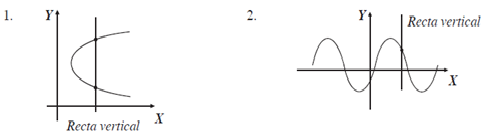
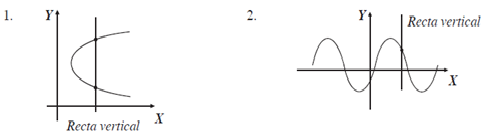
EJERCICIOS 1
Identifica si los siguientes conjuntos representan funciones o relaciones.
1.= \left\lbrace(0,3),(2,3),(-1,3)...\right\rbrace
2.= \left\lbrace(-3,5),(3,5),(-3,2)...\right\rbrace
3.= \left\lbrace(4,7),(-4,\sqrt{3}),(\sqrt{2},5)...\right\rbrace
4.= \left\lbrace(2,5),(\sqrt{4},2),(3,-3)...\right\rbrace
5.= \left\lbrace(a,2a),(-2a,3a),(4a,a)...\right\rbrace
6.= \left\lbrace(\cfrac{3}{2},1),(\cfrac{6}{4},-1),(1,\cfrac{5}{2})...\right\rbrace
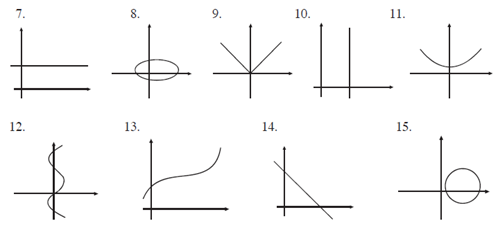
Identifica qué representa cada gráfica (función o relación):

Notación
Una función se denota o escribe como y=f(x) donde:
x: variable independiente
y: variable dependiente
f: función, regla de asignación o correspondencia.
Clasificación:
Las funciones se clasifican en: algebraicas y trascendentes


Ejemplos:
Algebraicas
Trascendentes
| f(x)=cos x | f(x)=e^{4x} | s(t)=ln(2t-4) |
| f(x)=sen(x-\frac{\pi}{2}) | y=e^{\sqrt{x}}+2 | g(x)= log(x+1) |
Las funciones algebraicas y trascendentes pueden ser:
• Explícitas.– Es cuando la función está en términos de una variable, por ejemplo:
| y=x^2 | f(x)=\cfrac{x-3}{x+5} | y=sen3x | s(t)=e^t | y=log x |
| y=x^3-1 | g(x)=\sqrt{\frac{x}{x-1}} | f(x)=cos \frac{1}{2}x | f(g)=2^{x+3} | f(x)=ln(3x) |
• Implícitas.– Es cuando ambas variables forman parte de la ecuación, por ejemplo:
|
x^2-8y+16=0 |
x^3+y^2-3x=0 | sen x+cos y =1 | e^y=x+3 |
Valor de una función (o evaluación de funciones).
El valor real f (x) de una función es aquel que toma “y” cuando se asigna a x un determinado valor real.
1.- Obtén f(-3)para f(x)= 3x^2-5x-2
Solución:
Para obtener f (-3) se sustituye x = -3 en la función y se realizan las operaciones indicadas,
f(-3)=3(-3)^2-5(-3)-2=27+15-2=40
Por tanto f (-3) = 40, es decir y = 40 cuando x = -3 o lo que es lo mismo, la curva pasa por el punto (-3, 40) en el plano cartesiano.
2.- f(x)=\cfrac{3x-1}{5-x} encuentre f(\cfrac{3}{4})
Solución:
Se sustituye x=\cfrac{3}{4} en la función y se realiza las operaciones:
f(\cfrac{3}{4})=\cfrac{3(\cfrac{3}{4})-1}{5-\cfrac{3}{4}}=\cfrac{\cfrac{9}{4}-1}{5-\cfrac{3}{4}}=\cfrac{\cfrac{5}{4}}{\cfrac{17}{4}}=\cfrac{5}{17} , por tanto, cuando x=\cfrac{3}{4}, f(\cfrac{3}{4})=\cfrac{5}{17}
3.- Si s(t)=\sqrt{t-5}, determinar s(4), s(a+5)
Solución
s(4)=\sqrt{4-5}=\sqrt{-1},la función no está definida para t=4 \sqrt{-1} no tiene solución real
s(a+5)=\sqrt{a+5-5}=\sqrt{a}
4.- Si f(x)=sen(x+\cfrac{\pi}{4}), determina f(\cfrac{\pi}{3})
Solución
Se sustituye x=\frac{\pi}{3} en f(x) y se utiliza la identidad sen( \alpha + \beta)= sen \alpha cos \beta + sen \beta cos \alpha


5.- Determinar \cfrac{f(a+b)-f(a)}{b} si f(x)=\sqrt{x}
Solución:
Se obtiene que f(a+b)=\sqrt{a+b} y f(a)=\sqrt{a}
Se sustituyen los valores obtenidos: \cfrac{f(a+b)-f(a)}{b}=\cfrac{\sqrt{a+b}-\sqrt{a}}{b}
Un resultado equivalente se obtiene al racionalizar el numerador:
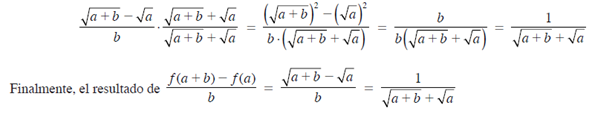
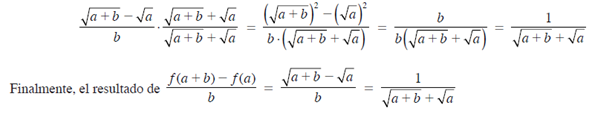
6.- Si y=\cfrac{x}{x+2} encuentra el valor de y cuando x=-2
Solución:
Al evaluar la función en x=-2
y=\cfrac{-2}{-2+2}=-\cfrac{2}{0}
La función no está definida para x=-2 , ya que la división entre cero no está determinada
Apunte Algunos Tipos de Funciones
Función constante
f(x)= k con k \in R representa una recta paralela al eje “X” sobre k.
Dominio D_f =R o bien x \in (-\infty, \infty ) \text{ Rango:} R_f ={k}


Ejemplo
Obtén la gráfica de f(x)= 4
Solución
Se traza una recta paralela al eje X sobre y= 4
D_f = R
R_f = {4}
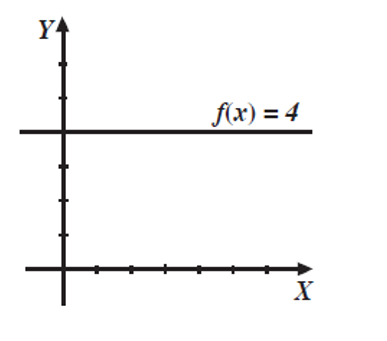
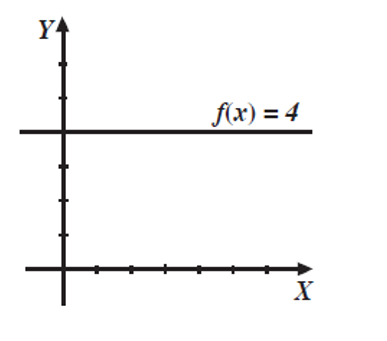
Función Lineal
Esta función tiene la forma f(x) = mx + b y representa una recta en el plano cartesiano, en donde m es la pendiente y b la ordenada al origen.
Dominio: D_f=R o bien x \in (-\infty, \infty),


Rango: R_f=R o bien \in (- \infty, \infty)


Para graficar una función lineal se lleva a cabo lo siguiente:
I. Se localiza la ordenada al origen, es decir, el punto (0 , b).
II. A partir de este punto, se localiza otro, tomando la pendiente como el incremento o decremento vertical sobre el incremento horizontal
Ejemplo
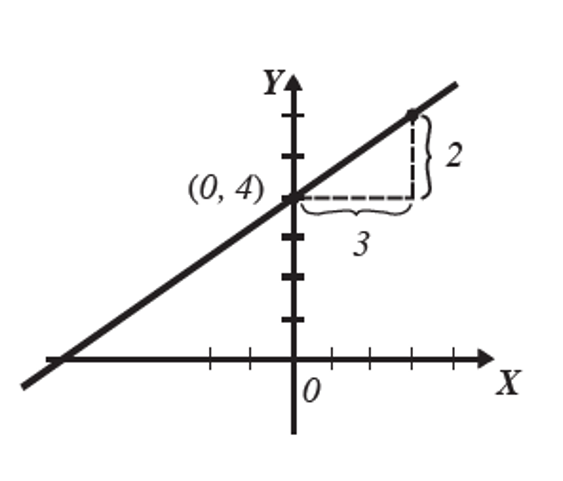
Grafica la Función y= \cfrac{2}{3}+4
Solución
La pendiente y la ordenada al origen de la función:
y= \cfrac{2}{3}+4
m= \cfrac{2}{3} \Longrightarrow \cfrac{\text{2 incremento vertical}}{\text{3 incremento horizontal} } , b= 4 representa el punto (0,4)
Gráfica de la función

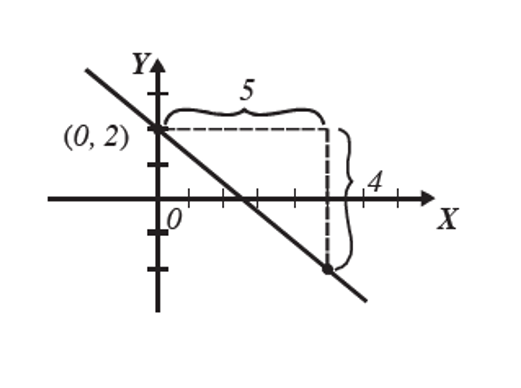
Traza la gráfica de la función y= -\cfrac{4}{5}x+2
Solución
La pendiente y la ordenada al origen de la función:
m =-\cfrac{4}{5}=\cfrac{-4}{5} \Longrightarrow \cfrac{\text{-4 decremento vertical}}{\text{5 incremento horizontal}} , b=2, \text{representa el punto (0,2)}
Gráfica de la Función

Función Identidad
Es la función lineal f(x)=mx + b, \text{con } m=1 \text{y } b=0, \text{ es decir: } f(x)=x
Dominio: D_f=R \text{ o bien } x \in (-\infty. +\infty) \text{ Rango: } R_f = R \text{ o bien } y \in (-\infty,+\infty)


Función Cuadrática
Es de la forma f(x)=ax^2+bx +c y representa una parábola cóncava hacia arriba o hacia abajo
\text{Si a} > 0
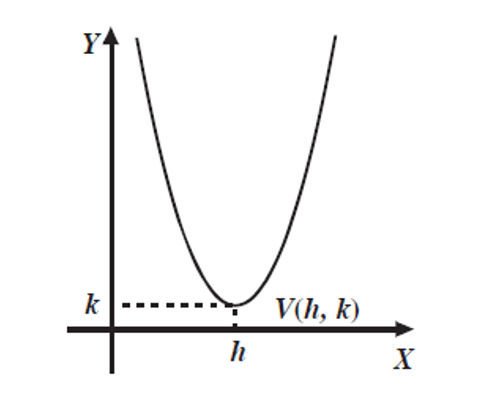

\text{Si a} < 0
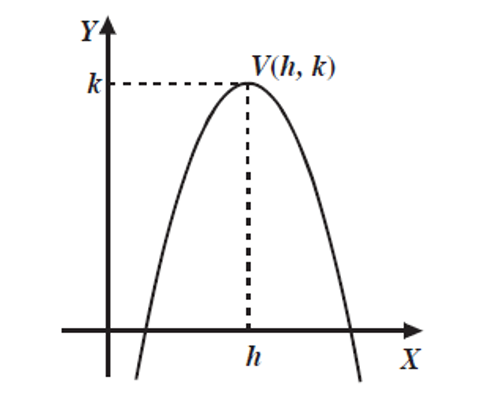

V(h,k): son las coordenadas del vértce.
Dominio: D_f =R \text{ o bien } x \in (-\infty, \infty)
Rango: y \in [\cfrac{4ac-b^2}{4a},\infty)
Dominio: D_f =R \text{ o bien } x \in (-\infty, \infty)
Rango: y \in -\infty, [\cfrac{4ac-b^2}{4a})
Para obtener las coordenadas (h,k) del vértice se aplican las siguientes fórmulas:
h= -\cfrac{b}{2a} , k=\cfrac{4ac-b^2}{4a}
Ejemplo:
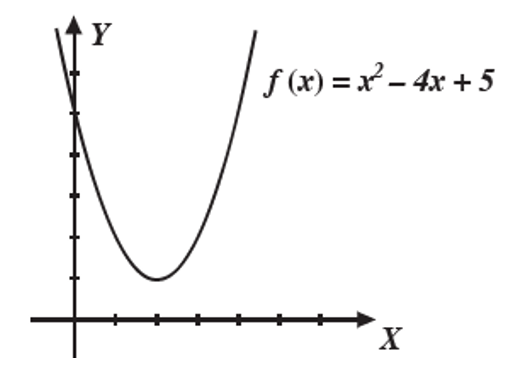
Obtener el dominio, rango y la gráfica de la función f(x)= x^2 -4x+5 .
Solución
Se identifican los valores de los coeficientes de cada término: a=1, b= -4 \text{ y } c=5.
a>0, \text{la parábola es cóncava hacia arriba}
Se calcula los valores de h y k:
h=-\cfrac{b}{2a} = \cfrac{-(-4}{2(1)} = 2; k=\cfrac{4ac-b^2}{4a} = \cfrac{4(1)(5)-(-4)^2}{4(1)} = 1
Para graficar, se tabula y se asignan valores de x menores y mayores que 2
| x | 0 | 1 | 2 | 3 | 4 |
| y | 5 | 2 | 1 | 2 | 5 |

La Función f(x)=x^n
Con “n” entero positivo tiene como: Dominio x \in (-\infty, \infty) es decir el conjunto de los reales R y Rango:


Obtén la gráfica de las funciones f(x)=x^3\text{ y } g(x)=x^5
Solución:
Se tabula para valores arbitrarios de x:
| x | -2 | -1 | 0 | 1 | 2 |
| f(x)=x^3 | -8 | -1 | 0 | 1 | 8 |
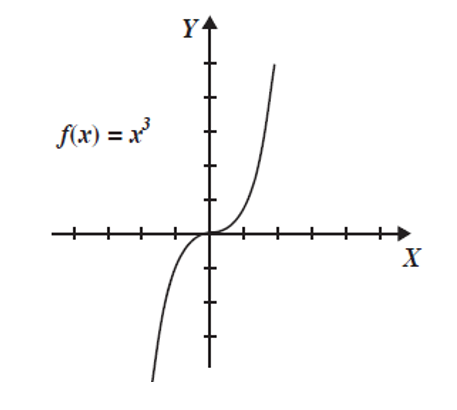
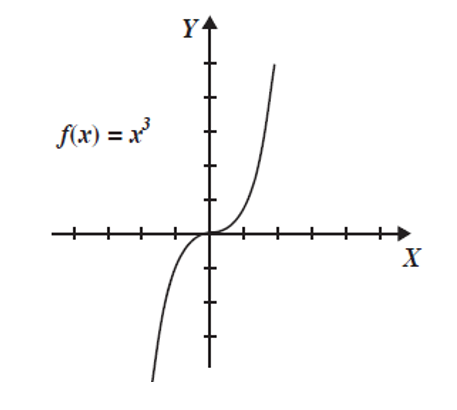
| x | \cfrac{3}{2} | -1 | 0 | 1 | \cfrac{3}{2} |
| g(x)=x^5 | \cfrac{243}{32} | -1 | 0 | 1 | \cfrac{243}{32} |


Función Racional
Se expresa como el cociente de dos funciones polinomiales
F(x)=\cfrac{P(x)}{ Q(x)}, \text{ con } Q(x)\neq 0
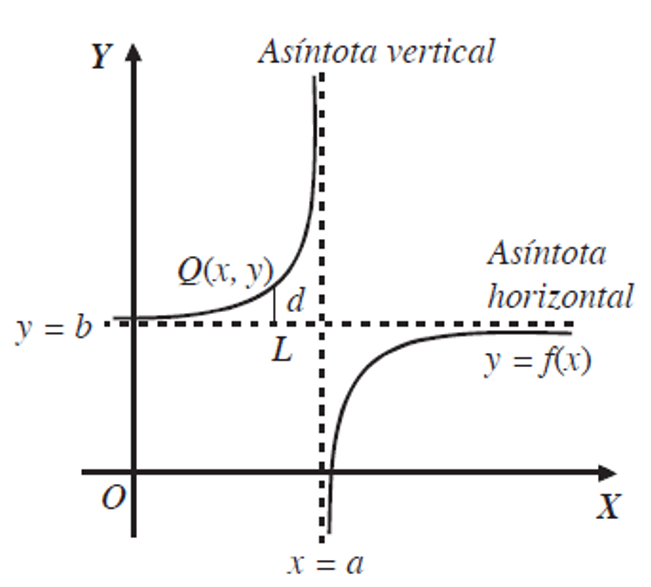
Definición de Asíntota
Si la distancia d entre una recta o curva L y el punto móvil Q(x,y) de la función tiende a cero, entonces la recta o curva recibe el nombre de asíntota.
Existen tres tipos de asíntotas: Verticales, Horizontales y Oblicuas
Cuando la gráfica de la función f(x) se acerca a la curva o recta L(x) y la distancia d entre un punto de f(x) y la curva o recta L(x) tiende a cero (es decir la gráfica no toca a L(x) ), entonces L(x) recibe el nombre de asíntota.
Asíntotas Verticales
Una Función de la forma F(x)=\cfrac{P(x)}{Q(x)} , tiene asíntotas verticales si existen valores x_1,x_2,x_3,....,x_n tal que se cumple lo siguiente:
Q(x_1)=Q(x_2)=...=Q(x_n) =0
Asíntotas Horizontales
Se despeja la variable independiente x, si se obtiene una función de la forma G(y)=\cfrac{R(y)}{S(y)} , tal que para los valores de y_1,y_2,y_3...y_n se cumpla que:
S(y_1)=S(y_2)=...=S(y_n)=0
Ejemplo



Función Raíz Cuadrada
La función está dada por: f(x)= \sqrt{g(x)}, \text{con } g(x) \geqslant 0
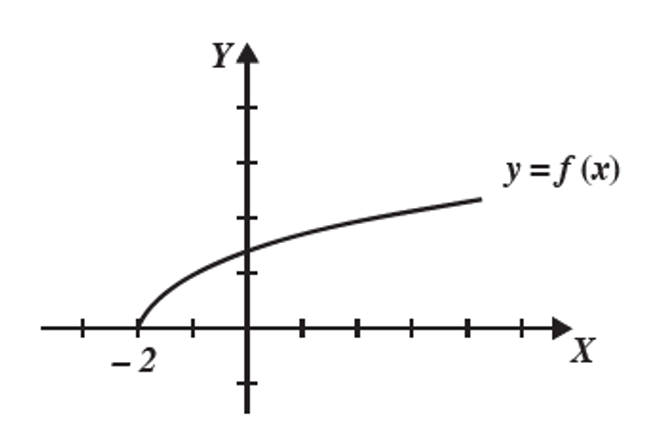
Obtén la gráfica de la Función f(x)= \sqrt{x+2}
Solución
Para determinar el dominio se resuelve la desigualdad x+2\geqslant 0 \text{ donde } x \geqslant -2 , entonces el dominio es el conjunto: \{ x \in R | x \geqslant -2 \} \text{ o } x \in [ -2, \infty)
El rango se obtiene despejando x
y= \sqrt{x+2} \longrightarrow y^2=x+2 \longrightarrow x=y^2-2
La función es una raíz positiva, o cero, es decir \in [0, \infty) y el despeje da como resultado una expresión polinomial donde y \in R , por tanto está defiido para y \in [0, \infty)
al tabular dando algunos valores en el intervalo x \in [-2, \infty) se obtiene:
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| f(x) | 0 | 1 | \sqrt{2} | \sqrt{3} | 2 | \sqrt{5} | \sqrt{6} | \sqrt{7} |
La Gráfica que se obtiene es:

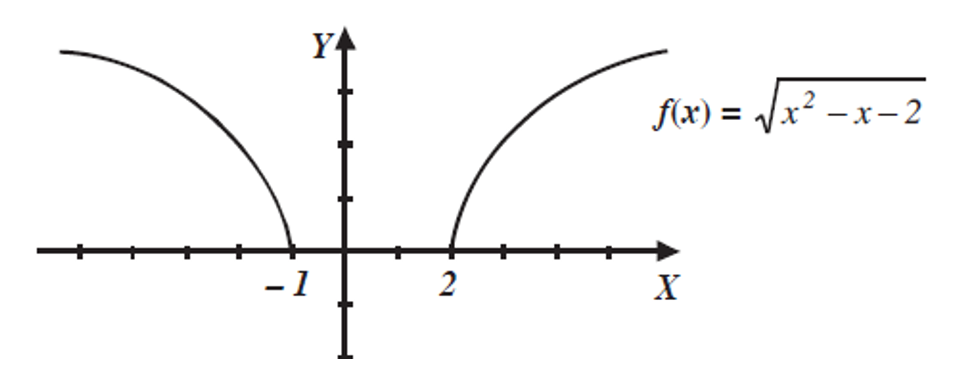
Determina la gráfica de la Función f(x)=\sqrt{x^2-x-2 }
Solución
Para obtener el dominio se resuelve la desigualdad x^2 -x-2\geqslant 0 obteniendo que
x \in (-\infty, -1 ] \cup [2,\infty)
Al despejar x se obtiene , x=\cfrac{1 \pm\sqrt{4y^2+9}}{2} donde y \in (-\infty, \infty), f(x) es una raíz positiva, o cero, por tanto el rango es: y \in (-\infty, \infty) \cap [0,\infty)=[0, \infty)

Grafica la Función y = \sqrt{\cfrac{x-1}{x+1}}
Solución
Para obtener el dominio se resuelve la desigualdad \cfrac{x-1}{x+1}\geqslant 0, obteniendo que:
x \in (-\infty, -1) \cup[1, \infty)
Al despejar x para obtener el rango:
y= \sqrt{\cfrac{x-1}{x+1}}\longrightarrow y^2=\cfrac{x-1}{x+1}\longrightarrow y^2 (x+1)=x-1
\longrightarrow y^2x+y^2=x-1
y^2x-x=-1-y^2
x(y^2-1)=-1-y^2
x=\cfrac{-1-y^2}{y^2-1} \text{, dónde } y \neq \pm 1
La función es una raíz positiva, y \in [0, \infty), entonces el rango corresponde a:
y \in [0, 1) \cup (1,\infty)
La función tiene una asíntota vertical en x=-1 y dos horizontales en y =-1, y=1, al graficar se obtiene:
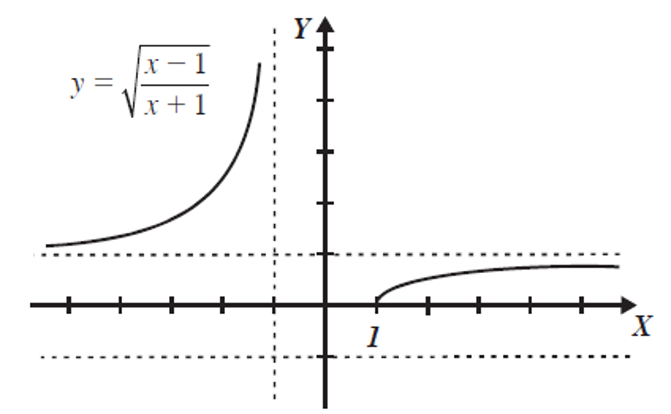

Nota: Observe que gráficamente y = -1 No es asíntota.
