Curso de Probabilidad y Estadística del Semestre 2021A página de Tareas Avisos, Apuntes y Material de Apoyo para las clases por Meet.
Índice del Contenido
Temario Probabilidad y Estadística.
UNIDAD 1 ESTADÍSTICA DESCRIPTIVA.
1.1 Introducción a la estadística.
1.2 Definición de estadística descriptiva y estadística inferencial.
1.3 Concepto de población y muestra.
1.4 Tipos de muestreo.
1.5 Fuentes de información.
1.6 Representación gráfica de datos.
1.6.1 Histograma.
1.6.2 Polígono de frecuencias.
1.7 Medidas de tendencia central para datos no agrupados y agrupados.
1.7.1 Media, Mediana y Moda.
1.8 Medidas de posición para datos agrupados. Cuartiles, Deciles., Percentiles.
1.9 Medidas de dispersión para datos no agrupados y agrupados.
1.9.1 Rango, Varianza, Desviación estándar, Coeficiente de asimetría y curtosis.
UNIDAD 2 PROBABILIDAD.
2.1 Teoría de conjuntos.
2.1.1 Notación de conjuntos y representación gráfica.
2.1.2 Unión, intersección, diferencia, complemento.
2.1.3 Álgebra de conjuntos.
2.2 Técnicas de conteo, Principio aditivo, Principio multiplicativo, Factorial, Permutaciones,
Combinaciones Diagramas de árbol.
2.3 Teoría de las probabilidades.
2.3.1 Enfoque clásico.
2.3.2 Enfoque frecuencial.
2.3.3 Espacios equiprobables y no equiprobables.
2.3.4 Espacios muestrales uniformes no contables.
2.4 Teoría axiomática de la probabilidad.
2.4.1 Axiomas de probabilidad.
2.5 Probabilidad condicional.
2.5.1 Espacio muestra reducido.
2.5.2 Definición de probabilidad condicional.
2.6 Probabilidad de eventos dependientes e independientes.
2.6.1 Eventos dependientes.
2.6.2 Eventos independientes.
2.6.3 Teorema de la multiplicación.
2.7 Probabilidad de eventos estocásticos finitos.
2.8 Teorema de Bayes.
UNIDAD 3 DISTRIBUCIONES DE PROBABILIDAD.
3.1 Variables aleatorias discretas, y continuas.
3.2 Valor esperado y desviación estándar para variables aleatorias discretas y continuas.
3.3 Distribuciones de probabilidad con nombre propio.
3.3.1 Distribución binomial.
3.3.2 Distribución de Poisson.
3.3 3 Distribución normal.
3.3.4 Aproximación normal a la distribución binomial.
Tareas
En esta sección se publicarán las tareas para entregar en el Semestre
Avisos
Calendario del Semestre con las fechas importantes!!
Material de Apoyo
Material de apoyo para las clases en línea
UNIDAD 1 ESTADÍSTICA DESCRIPTIVA.
Ejemplo:
En un centro comercial, se consultó la edad a todas las personas que entraban entre las 12:00 h y 12:30 h. Los resultados obtenidos fueron los siguientes:
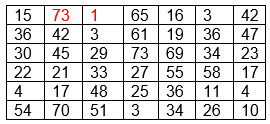

Construye una tabla de frecuencias cuyos datos estén agrupados en ocho intervalos.
Solución:
1) Para poder construir la tabla de frecuencias lo primero que debemos hacer es calcular el rango.
El dato mayor y el menor lo he destacado con color rojo:
Dato mayor – dato menor = 73 – 1 = 72
Por lo tanto; Rango = 72
En el problema nos dicen que debemos agruparlo en 8 intervalos o clases, con este dato podemos calcular la amplitud o tamaño de cada intervalo, dividiendo el valor del rango por la cantidad de intervalos que se desean obtener (en este caso son 8).
Amplitud: La amplitud de un intervalo es la diferencia entre el límite superior y el límite inferior. La amplitud (i) de los intervalos puede calcularse:
i=\cfrac{72}{8}=9 Por lo tanto la amplitud de cada intervalo será de 9
2) Ahora podemos comenzar a construir la tabla de frecuencias:
Hay distintas formas de construir los intervalos dependiendo del tipo de variable que estemos trabajando
a) Variables cuantitativas discretas: sólo pueden tomar un número finito de valores. Siendo por lo general estos valores los números naturales 1, 2, 3…Un ejemplo son el número de hijos, el número de habitaciones de una vivienda, el número de matrimonios de una persona. Cuando categorizamos variables discretas los límites de clase son idénticos a los límites reales. Por ejemplo, el número de personas que viven en una familia podemos agruparlo, De 1 hasta 2 (0 es imposible no hay ninguna familia sin ningún miembro) De 3 hasta 4, De 5 hasta 7.
b) Variables cuantitativas continuas: Las variables continuas, por el contrario, pueden, tomar un número infinito de valores en cualquier intervalo dado. En este caso los valores se agrupan en intervalos cuyos límites inferior y superior serían los siguientes:
Inferior: L_{i} ; Superior L_{s}
Habitualmente, los intervalos se consideran cerrados a la izquierda y abiertos a la derecha, es decir que el extremo inferior está incluido en el intervalo, pero el extremo superior no.
Es importante mencionar que las clases o intervalos para las variables continuas pueden ser de tres tipos:
Abiertas: clases abiertas tienen límites determinados (a,b), pero los valores que la contienen comprenden valores muy cercanos a estos límites sin comprenderlos a ellos mismos, esto se representa con un intervalo definido entre paréntesis ( ). Esto quiere decir que esta clase contiene valores desde a hasta b pero no contiene exactamente “a” ni “b” solo valores muy cercanos.
Cerradas: las clases cerradas, además de los valores que están entre a y b, los contiene a ellos, y se representa con corchetes [a, b].
Semiabiertas: pueden contener “a” o “b” más los valores que están entre ellos, y se puede representar con un corchete y un paréntesis, por ejemplo, (a,b], en este caso no contiene el valor a y si los valores de b, además de los valores que están entre estos.
c) Registro discretos de variables continuas: Cuando la variable considerada es continua pero ocurre que la precisión del instrumento de medida se limita a un número finito de datos, existe la opción de construir los intervalos de tal forma que ambos extremos estén incluidos en él.
Ejemplo: 50 a 52, 53 a 55, 56 a 58, 59 al 61 y 62 al 64
Estos serían los límites aparentes de los intervalos.
Con esta información construiremos la tabla en esta ocasión con el último método explicado.

Marca clase o centro de la clase: es la semisuma de los límites de cada clase. Representa a todos los datos que están contenidos en una clase.
Responder las siguientes preguntas:
a) Del total de personas encuestadas, ¿cuántas personas tienen entre 31 y 40 años?
Respuesta: Observamos los datos obtenidos en la tabla y tenemos que:


El dato lo obtenemos de la columna de la frecuencia absoluta.
Recuerda que:
Frecuencia absoluta.- Corresponde a la cantidad de veces que se repite un dato. Denotamos este valor por f_{i}
Por lo tanto la respuesta es 6 personas.
b) Del total de personas encuestadas, ¿cuántas personas tienen 60 o menos años?
Respuesta: Observamos los datos obtenidos en la tabla y tenemos que:


El dato lo obtenemos de la columna de frecuencia absoluta acumulada
Recuerda que:
Frecuencia absoluta acumulada es la suma de las frecuencias absolutas observadas hasta el intervalo i.
En este caso es el intervalo 6. Por lo tanto la respuesta es 36 personas tienen 60 o menos años.
c) ¿Cuál es la probabilidad de, que al elegir al azar a un persona consultada, esta tenga entre 11 y
Respuesta: Observamos los datos obtenidos en la tabla y tenemos que:


El dato lo obtenemos de la columna de frecuencia relativa.
Frecuencia relativa Corresponde a la probabilidad de pertenecer a cierta categoría. Se puede expresar en tantos por ciento.
En este caso es el intervalo 2, ya que es ahí donde se encuentran las edades entre 11 y 20 años.
Entonces la respuesta es: La probabilidad es 14%.
Por último vamos a repasar el concepto de:
Frecuencia relativa acumulada, Es la probabilidad de observar un valor menor o igual al valor que toma la variable en estudio en ese intervalo.
Se calcula dividiendo f_i por el número total de datos. También puedes calcularlo Sumando la
frecuencia relativa de cada grupo con la frecuencia relativa acumulada del grupo anterior.
Si haces correctamente estos cálculos, el último grupo tendrá una frecuencia acumulada de 1, o muy cerca de 1, permitiendo redondear el error.
Recuerda que este valor se puede expresar como porcentaje, para esto solo debes multiplicar el valor obtenido por 100 y listo.
Este cálculo te sirve en el caso de que te pregunten:
a) Si le preguntas a una persona cualquiera ¿Cuál es la probabilidad de que tenga 50 años o menos?


Respuesta: La probabilidad es de un 76%
REPRESENTACIONES GRÁFICAS
En estadística denominamos gráficos a aquellas imágenes que, combinando la utilización de sombreado, colores, puntos, líneas, símbolos, números, texto y un sistema de referencia (coordenadas), permiten presentar información cuantitativa. La utilidad, de los gráficos es doble, ya que pueden servir no sólo como sustituto a las tablas, sino que también constituyen por sí mismos una poderosa herramienta para el análisis de los datos, siendo en ocasiones el medio más efectivo no sólo para describir y resumir la información, sino también para analizarla.
TIPOS DE REPRESENTACIONES GRÁFICAS
En estadística existen muchos tipos de gráficas, pero las que utilizaremos serán las siguientes:
Histograma: forma especial de diagrama de barras para distribuciones cuantitativas continuas.
Polígonos de frecuencias: formados por líneas poligonales abiertas sobre un sistema de ejes cartesianos.
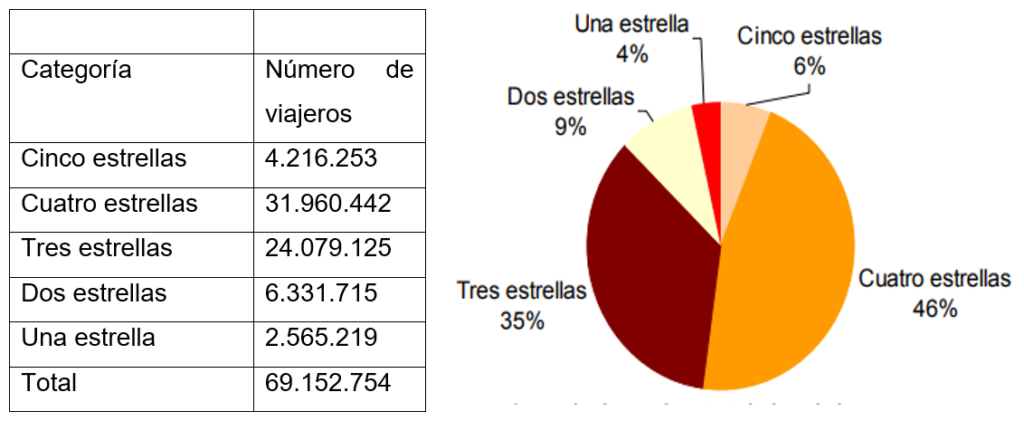
Gráficas circulares: dividen un círculo en porciones proporcionales según el valor de las frecuencias relativas.
Un gráfico circular es una representación de las frecuencias relativas de una variable cualitativa o discreta que permite, de una manera sencilla y rápida, su comparación. El círculo representa la totalidad que se quiere observar
Ejemplo: Una encuesta de ocupación en alojamientos turísticos de viajeros hospedados en hoteles españoles por categoría del establecimiento, se muestra en la siguiente tabla. ¿Hacer un diagrama circular?

Polígonos de frecuencias acumuladas.- Es el que se construye uniendo los puntos medios de las cúspides de las barras del histograma.
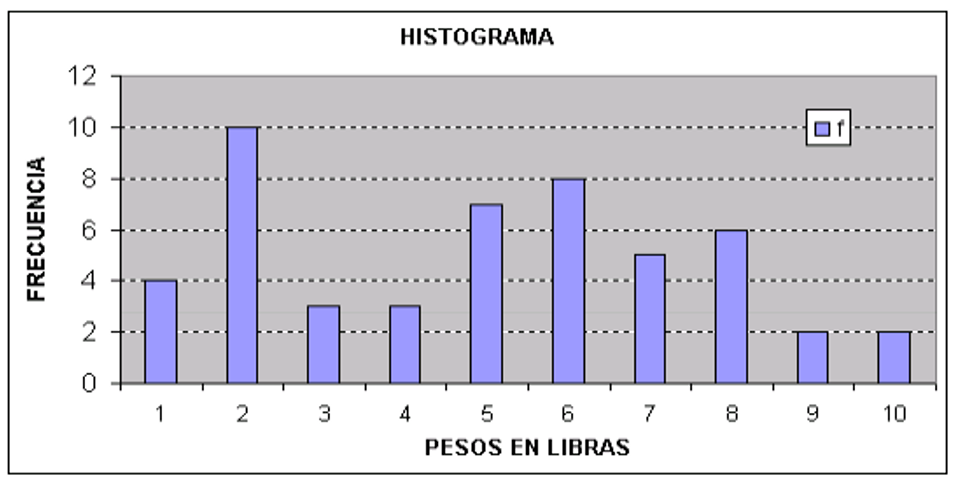
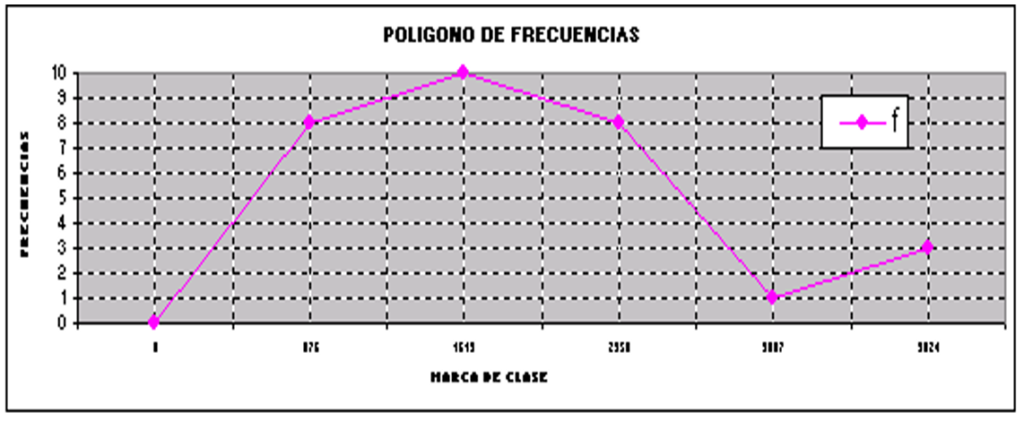
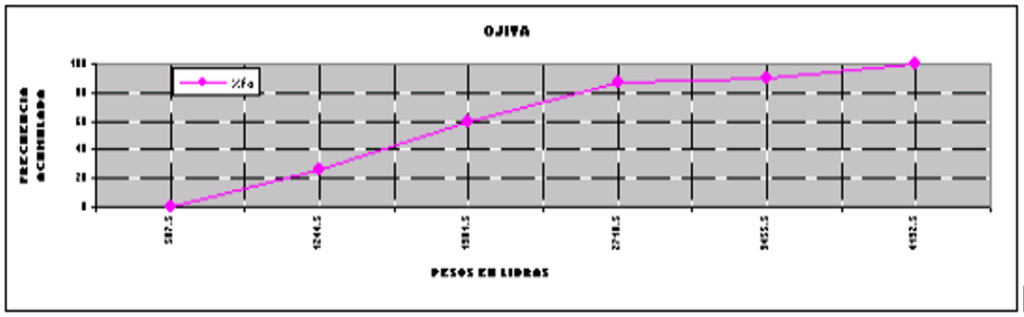
Ejemplo. Ordena los datos de la tabla siguiente, recolectados de los pesos (en lbs.) de cincuenta estudiantes, para diez clases o intervalos. Traza el histograma, polígono de frecuencias y polígono de frecuencias acumuladas o también llamada ojiva.


Solución:
1) Para poder construir la tabla de frecuencias lo primero que debemos hacer es calcular el rango.
Dato mayor – dato menor = 215 – 98 = 117
Por lo tanto; Rango = 117
2) En el problema nos dicen que debemos agruparlo en 10 intervalos o clases, con este dato podemos calcular la amplitud o tamaño de cada intervalo, dividiendo el valor del rango por la cantidad de intervalos que se desean obtener (en este caso son 10).
a=\cfrac{117}{10}=11.7 \approx 12
El ancho de clase se ajusta a conveniencia para abarcar todos los datos. Para asegurarnos de que ningún valor quede fuera definiremos un nuevo rango de los datos, multiplicando el número de intervalos por el ancho de cada clase, NR = 10 (12)=120, como es mayor del rango que teníamos por 3 unidades, le quitamos 2 al límite inferior y le sumamos uno al límite superior:
Para el valor menor será L_{i}=98-2=96 ; y para el valor mayor será L_{s}=215 +1 =216
Finalmente, para obtener la frecuencia de cada clase se cuenta el número de datos que quedan entre sus límites. En el caso de que un dato se encuentre en la frontera de una clase, se debe contar en la siguiente clase y no en la anterior.


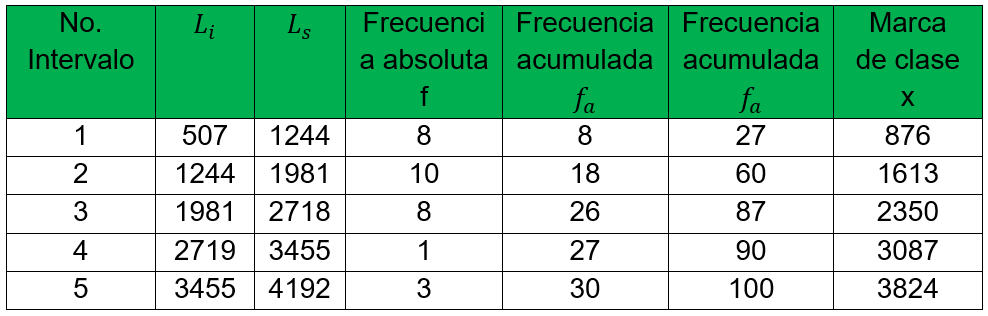
En donde: L_{1} y L_{2} son los límites inferior y superior, f es la frecuencia absoluta, f_{a} es la frecuencia absoluta acumulada, frecuencia relativa acumulada en porcentaje y por último x que es la marca de clase.
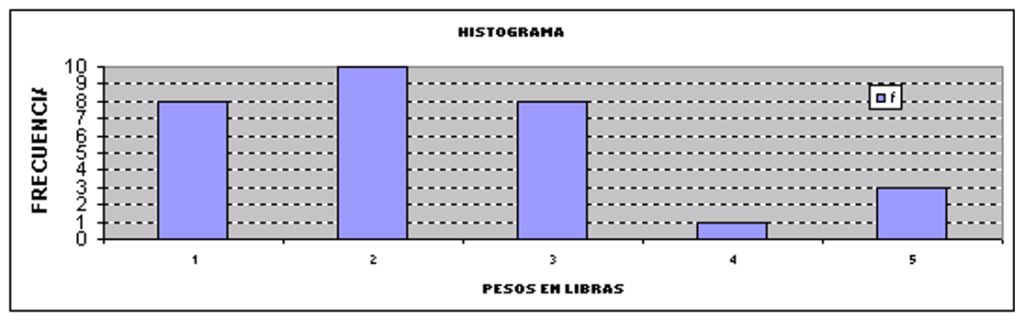
A continuación se procede a elaborar las gráficas a partiendo de la información que se ha obtenido en la tabla de distribución de frecuencias. Las gráficas que se realizarán son: histograma, polígono de frecuencias y polígono de frecuencias acumuladas.
Histograma.- Es el tipo de gráfica las barras representan la forma en que están distribuidas las frecuencias. En el eje de las abscisas se colocan los puntos medios de los intervalos o marcas de clase. En el eje de las ordenadas se colocan las frecuencias (absolutas o relativas).

Polígono de frecuencias.- Es una gráfica de líneas que sirve para representar la distribución de datos continuos. Se utiliza para ver la forma de la distribución de los datos, así como la ubicación de la mayor concentración de estos. Y para trazarla se utiliza sistema rectangular, marcando un punto por cada coordenada, en el eje de las abscisas se coloca la marca de clase y en el de las ordenadas las frecuencias absolutas o relativas.
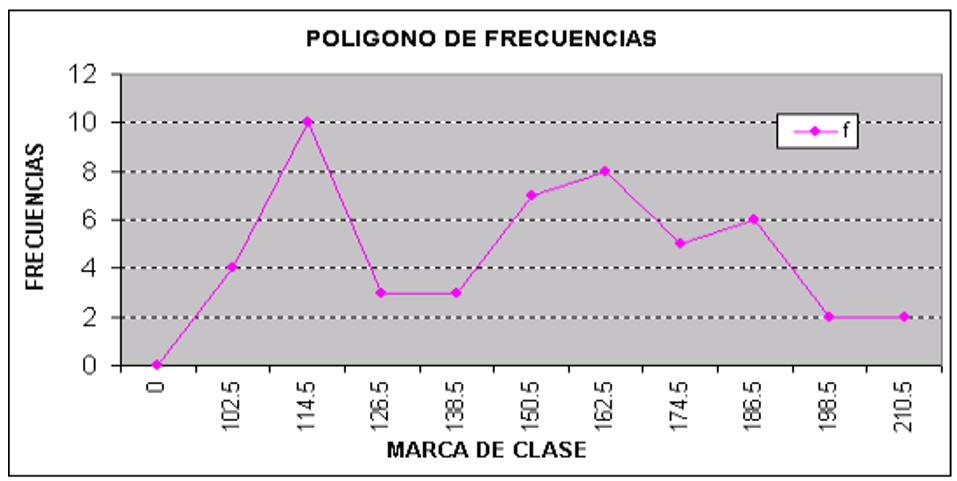

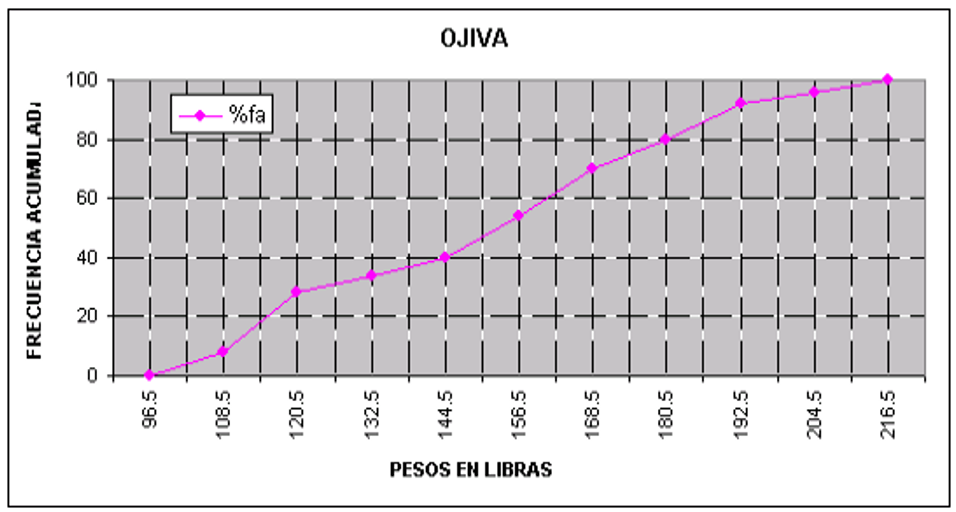
Polígono de frecuencias acumuladas o también llamado ojiva.– Para trazar se apoya con un sistema rectangular colocando las frecuencias acumuladas en el eje de las ordenadas, en el eje de las abscisas se inicia con el límite inferior disminuido y se continúa con el límite superior real o el disminuido de cada clase o intervalo. Uniendo los puntos así obtenidos obtenemos el polígono buscado.

Ejercicio. Se tomó una muestra de 30 personas y se les preguntó cuánto ganaban a la quincena, los datos son:


Si nos dan un ancho de clase de 737, ¿cómo será las distribuciones de frecuencia.
Solución:
1) Para poder construir la tabla de frecuencias lo primero que debemos hacer es calcular el rango.
Dato mayor – dato menor = 4190 – 510 = 3680
Por lo tanto; Rango = 3680
Calculamos los intervalos: NC =\sqrt{30}=5.47 \sim 5
2) Como la amplitud de cada intervalo ya nos la dan y es de 737
a=737
De acuerdo a estas condiciones el nuevo rango de los datos es:
NR = NC a = (5) 737 = 3685
Como salio mayor por 5 al rango calculado se le restan tres al límite inferior y se le suman dos al límite superior




MEDIDAS DE TENDENCIA CENTRAL
Un conjunto de datos puede conocerse numéricamente por medio de algunas medidas que lo describen; por ejemplo, la media y la desviación estándar, entre otras. De esta manera, es posible comparar entre sí varios grupos de datos.
Hay dos tipos de medidas: las de tendencia central o posición y las de dispersión o de variabilidad. Entre las primeras destacan la media o promedio, la mediana y la moda, en tanto que las de dispersión más comunes son el rango, la varianza y la desviación estándar.
PARA DATOS NO AGRUPADOS.
Media.– Es el valor promedio de datos, si es de una población se representa con la letra griega mu (μ) y si es de una muestra de objetos como \bar{x}. Para calcular la media:
\mu=\cfrac{\sum f_{ix_{i}}}{n} o \bar{x}=\cfrac{\sum f_{ix_{i}}}{n}
Donde x_{i} representa el valor de cada dato, f_{i}representa la frecuencia de cada dato y la letra ( \sum ) indica sumar todos los resultados de las multiplicaciones.
Mediana: Es el valor del elemento que ocupa la posición central cuando los datos se ordenan de menor a mayor, y se representan como \bar{x}.
Se pueden presentar dos situaciones: Cuando el número de datos es impar, la mediana es el dato que ocupa exactamente la posición central y cuando el número de datos es par, la mediana es el promedio de los dos datos que se encuentran en el centro.
Moda.- Es el valor de x que ocurre con mayor frecuencia o el que más se repite.
PARA EL CASO DE DATOS AGRUPADOS
La fórmula es la misma para la media, la diferencia está en el valor de ahora corresponde a la marca de clase, es decir
\mu=\cfrac{\sum f_{ix_{i}}}{n} o \bar{x}=\cfrac{\sum f_{ix_{i}}}{n}
Para la mediana es: \tilde{x}=L_{i}+\cfrac{\frac{n}{2}-f_{a}}{fm}(a)
Dónde:
L_{i}= Es el límite inferior de la clase mediana, que es la clase donde se acumula la mitad de los datos.
n=Es en número total de datos
f_{a}= Es la frecuencia acumulada antes de la clase mediana.
f_{m}= Es la frecuencia de la clase mediana
a=Es el ancho de la clase mediana.
La fórmula para calcular la moda es: \hat{x} =L_{i}+( \cfrac{\triangle_{1}}{\triangle_{1}+\triangle_{2}} )(a)
L_{i}= Es el límite inferior de la clase modal, que es la clase donde se acumulan la mayor cantidad de los datos.
\triangle_{1} Esa la diferencia entre las frecuencias de la clase modal y la clase anterior.
\triangle_{2} Es la diferencia entre las frecuencias de la clase modal y la clase posterior.
a Es el ancho de la clase modal.
Ejemplo: Obtener la media, mediana y moda de 100 estudiantes que fueron entrevistados para identificar su nivel de dominio del inglés hablado de la siguiente tabla de frecuencias.
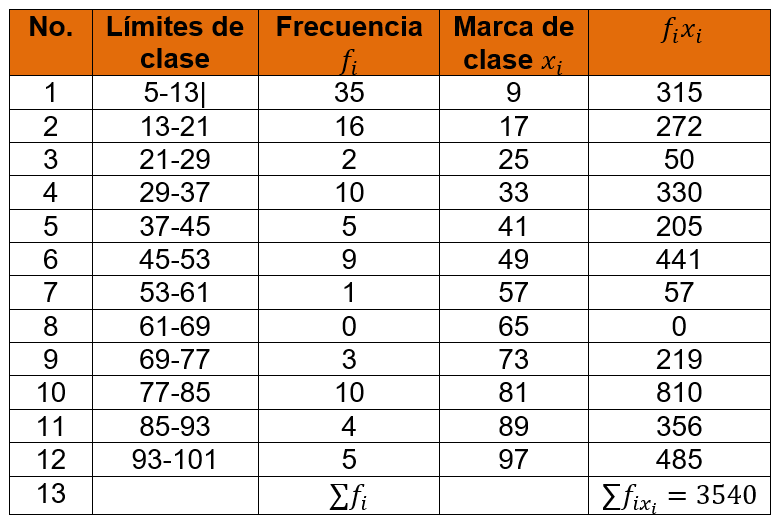

La media:
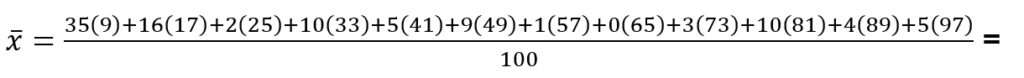
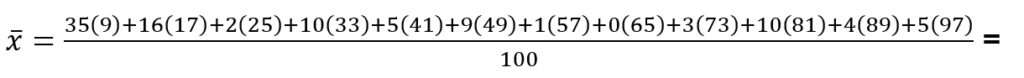
\bar{x}=\cfrac{3540}{100}=35.4
La media de 100 estudiantes que fueron entrevistados es de 35.4. Esto quiere decir que 35.4% de los alumnos hablan inglés.
La mediana es \tilde{x}=13+\left(\cfrac{50-35}{16}\right)8\rightarrow \tilde{x}=13+\left(\cfrac{15}{16}\right)8= \tilde{x}=13+7.5 por lo tanto \tilde{x}=20.5
\hat{x}=5+\left[ \cfrac{35}{35+19}\right] 8 \rightarrow \hat{x}=5+5\left[\cfrac{35}{54}\right]\rightarrow \hat{x}=5+5.18 por lo tanto \hat{x}=10.18
MEDIDAS DE POSICIÓN O UBICACIÓN
Así como la mediana marca la mitad de valores mayores que ella y la mitad de valores menores que ella los cuartiles permiten identificar valores ubicados en diferentes posiciones de un grupo de datos.
Los cuartiles 1°, 2° y 3° señalan el valor que está al 25, 50 y 75 % de la totalidad de datos, el segundo cuartil equivale a la mediana.
Los deciles del 1° al 9°, marcan el valor ubicado al 10,20,……80, y 90 % de los datos, el quinto decil equivale a la mediana.
Los percentiles del 1° al 99°, indican el valor que está al 1,2,……98, y 99% de los datos, el valor del cincuenta percentil deberá coincidir con el de la mediana.
Los deciles 1°, 2°,..etc., equivale a los percentiles 10°, 20°, etc., y los cuartiles equivalen a los percentiles 25, 50 y 75.
Cuartiles.- Dividen a los datos ordenados en cuatro partes iguales; cada conjunto de datos contiene cuatro cuartiles Q=\cfrac{n}{4}
Deciles.- Dividen a los datos ordenados en diez partes iguales; cada conjunto de datos contiene diez deciles D=\cfrac{n}{10}
Centiles o Percentiles.– Dividen en cien partes iguales a un conjunto de datos ordenados; tal conjunto tiene cien centiles C=\cfrac{n}{100}
Ejemplo
Calcular el segundo cuartil, el octavo decil y el 38 porcentil, del ejemplo de los pesos en libras de los 50 estudiantes. Además:
a) ¿Qué porcentaje de los estudiantes pesan más de 157 lbs?
b) ¿Qué porcentaje de los pesos debe disminuirse o incrementarse para tener una media de 155 lbs?
c) ¿Cuántos estudiantes tienen mayor peso, si el 28% de ellos son los más pesados?
d) ¿Qué porcentaje de los estudiantes tienen menor peso, si 17 de ellos son los más pesados?
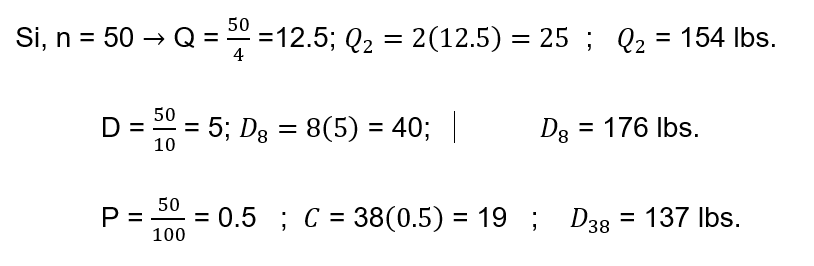
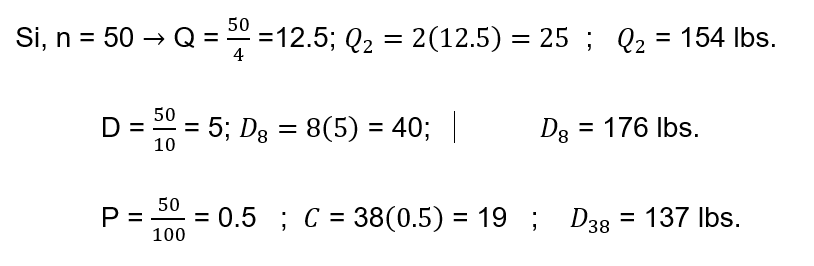
Por medio de reglas de tres se tiene:


Para el b) se calcula primero la media de la muestra con \bar{x}=\cfrac{\sum f_{ix_{i}}}{n}
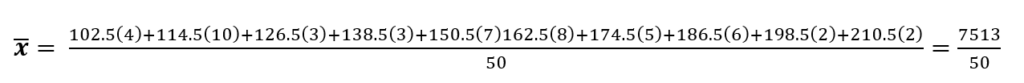
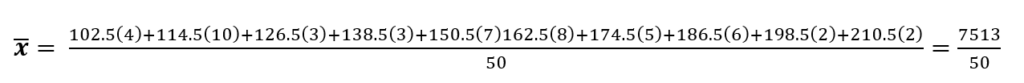
La media es x=150.26
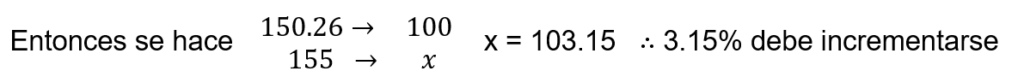
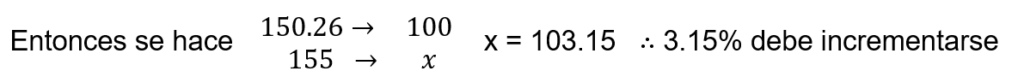


MEDIDAS DE DISPERSIÓN
Las medidas de dispersión es la manera en que los valores individuales de una muestra o población se desvían del valor promedio y abarcan:
Rango.- Corresponde a la identificación de la dispersión de los datos de una muestra, se calcula con la diferencia del dato mayor y el dato menor.
Varianza poblacional.- Es el promedio de los cuadrados de las diferencias que cada dato tiene con la media de la población (30 o más datos) y se calcula con:
\sigma^2=\cfrac{\sum(x_{i}-\mu)^2f_{i}}{n}
Dónde:
x_{i}=Marca de clase del intervalo
\mu=La media
f_{i}=Frecuencia absoluta
n= el tamaño de la muestra o número total de datos
Desviación estándar poblacional.- Es la raíz cuadrada de la varianza poblacional y se calcula con la fórmula:
\sigma=\sqrt{\cfrac{\sum(x_{i}-\mu)^2f_{i})}{n}}
Varianza muestral.- Es el promedio de los cuadrados de la diferencia de cada dato con la media de la muestra (menos de 30 datos) y se calcula con la fórmula:
s^2=\cfrac{\sum(x_{i}-\hat{x})^2f_{i})}{n}
Desviación estándar muestral.- Es la raíz cuadrada de la varianza muestral y se calcula con:
s^2=\sqrt{\cfrac{\sum(x_{i}-\hat{x})^2f_{i})}{n}}
Ejemplo:
Un industrial de bicicletas requirió analizar su producción de ejes de 110 milímetros de longitud, con una tolerancia de ± 1 mm. Como deseaba saber si su producción se ajustaba a las especificaciones, efectuó un muestreo con 50 ejes escogidos al azar.
1.- Calculamos el rango R = 113.1 – 108.6 = 4.5
2.- Calculamos el número de intervalos o clases NC =\sqrt{50}=7.07 \approx 7
3.- Calculamos el ancho de clase (amplitud) de cada intervalo a=\cfrac{4.5}{7}=0.64 \approx 0.7
4.- Calculamos un nuevo rango para asegurarnos que ningún dato quede fuera NR = 7 x 0.7 = 4.9 como el nuevo rango es mayor que el rango real, para compensar daremos un margen de 0.2 antes del menor dato y 0.2 después del mayor valor.
Quedando el menor valor como 108.4 y el valor mayor como 113.3.
5.- Se hace la tabla de frecuencias.
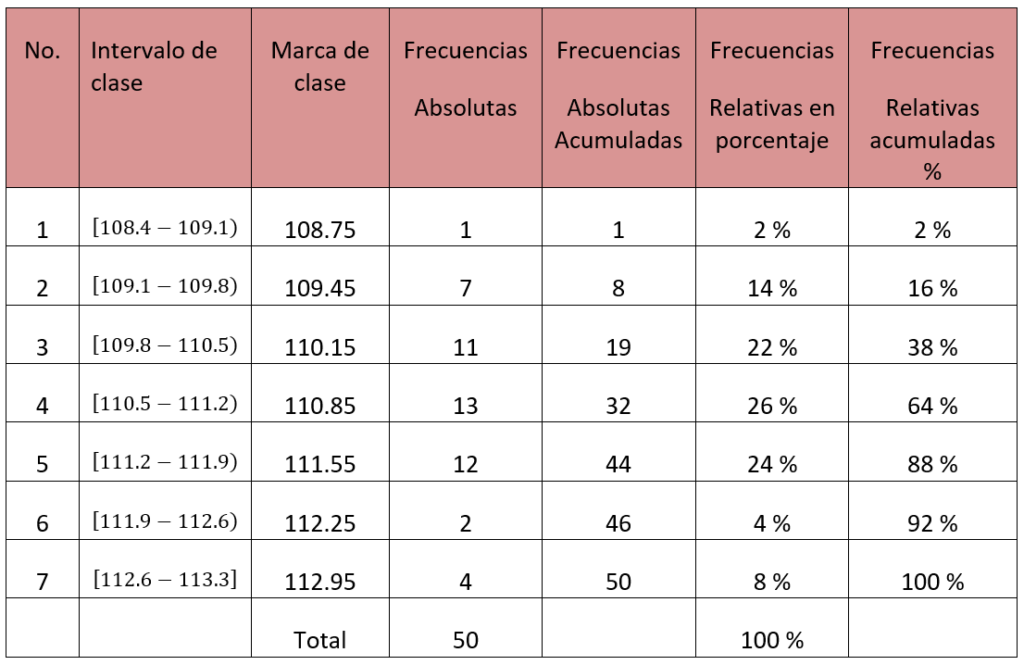

6.- Con la información de la tabla se traza el histograma, colocando en el eje de las abscisas la
marca de clases de cada intervalo y en eje de las ordenadas la frecuencia absoluta
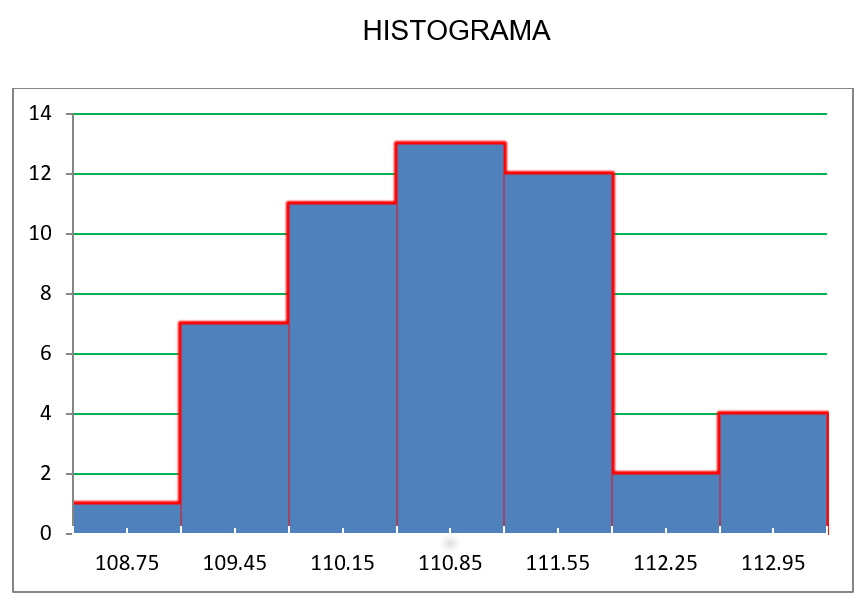

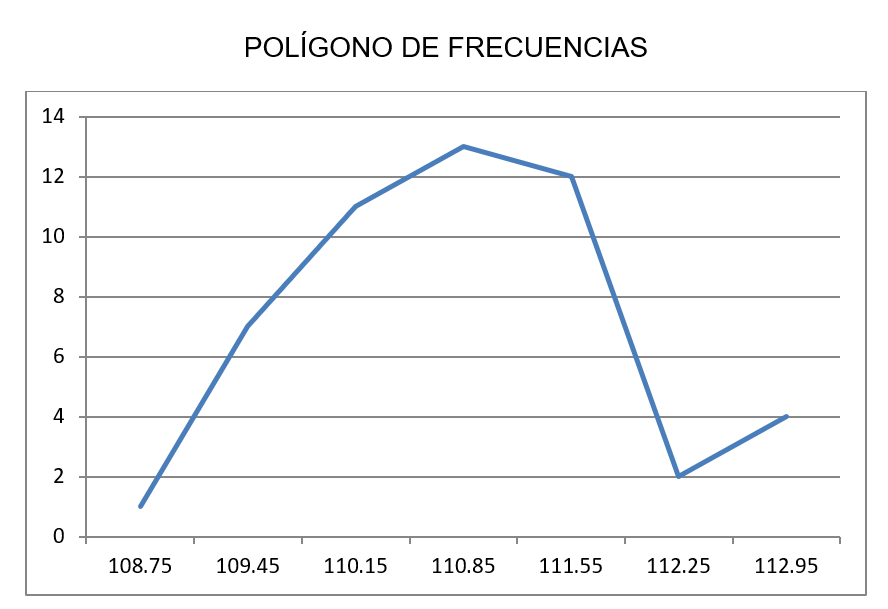

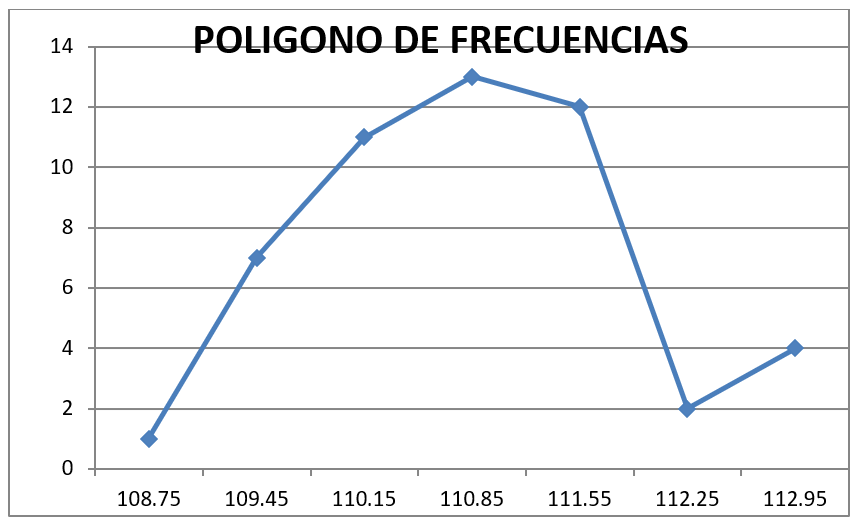

Medidas de tendencia central.- Media utilizaremos la formula siguiente ya que son objetos
\bar{x}=\cfrac{\sum f_ix_i}{n}
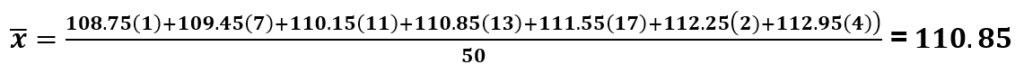
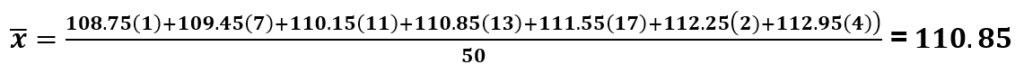
Mediana \tilde{x}=L_i+\cfrac{\cfrac{n}{2}-f_a}{f_m}(a)
\tilde{x}=110.5+\cfrac{\cfrac{50}{2}-19}{13}(0.7)=110.5+\cfrac{6}{13}0.7=110.5+0.32=110.82
Moda usaremos la fórmula \hat{x}=L_i +\left(\cfrac{\triangle_1}{\triangle_1+\triangle_2}\right)(a)
\hat{x}=110.5+\left(\cfrac{2}{2+1}\right)(0.7)=110.5+\left( \cfrac{2}{3}\right)0.7=110.5+0.46=110.9
Ahora calculamos las medidas de dispersión:
El rango ya lo calculamos al inicio del ejemplo y es R =113.1-108.6 = 4.5
La varianza se calcula con la fórmula \sigma^2=\cfrac{\sum(x_i-\tilde{x}^2f_i)}{n}
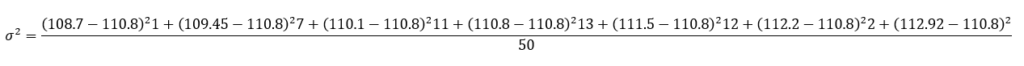
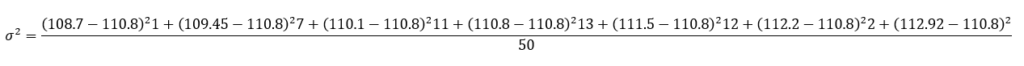
\sigma^2=\cfrac{50.21}{50}=1.004
Desviación estándar que es la raíz cuadrada de la varianza
\sigma^2=\sqrt{1.004}=1.001
Calculamos las medidas de posición utilizando la fórmula para datos agrupados
Cálculo del cuartil utilizando la fórmula:
Q_n=L_i+\left( \cfrac{\frac{Q_n}{4}-f_a}{f}\right)(a)
Donde
L_i es el límite inferior de la clase donde se encuentra cuartil deseado.
f_a es la frecuencia acumulada anterior a la clase mediana
f es la frecuencia absoluta
a es el ancho de intervalo
De nuestro ejemplo calcular el tercer cuartil primero se calcula el cuartil 1=\cfrac{Q_n}{4}=\cfrac{1(50)}{4}=(12.5)3=37.5 Buscamos el valor 37.5 en las frecuencias acumuladas, y se seleccionó el intervalo 44 por ser el más cercano superior ya que no se tiene exactamente 37.5 aplicamos la fórmula
Q_3=111.2+\left( \cfrac{37.5-32}{12}\right) 0.7 =111.5
Ahora calculamos el decil 2. Con \cfrac{50}{10}=5 luego lo multiplicamos por 2 quedando 10 y buscamos la clase donde se encuentra 10, en la tabla de frecuencias acumuladas y seleccionamos el 19 que es el más próximo superior y aplicamos la formula
D_n=L_i+\cfrac{\frac{kN}{10}-f_a}{f_i}(a) donde:
D_n es el decil que me solicitan
n indica el número de decil que se quiere calcular
L_i es la frontera inferior de la clase donde se encuentra el decil deseado
f_a es la frecuencia acumulada anterior
f_i es la frecuencia absoluta donde se encuentra el decil buscado.
D_n=109.8+\left(\cfrac{10-8}{11}\right) 0.7=109.9
Calculamos el percentil 78. Primero calculamos P_n=\cfrac{78(50)}{100}=39, buscamos el valor 39 en la frecuencia acumulada, por lo que se selecciona el intervalo con una frecuencia acumulada de 44.
P_{78}=111.2+\left( \cfrac{39-32}{12}\right)0.7=111.6
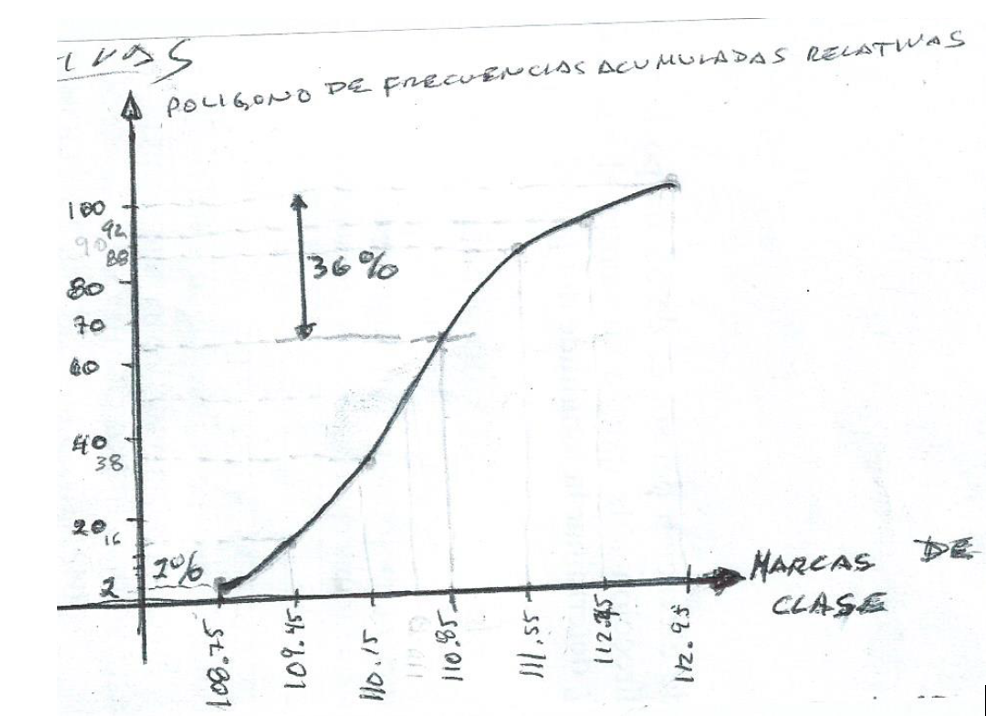

CONCLUSIONES: De La fabricación de ejes de bicicleta se observó viendo esta gráfica del polígono de frecuencias acumuladas que el 2% de los ejes tiene dimensiones menores y el 36% tiene dimensiones mayores a las requeridas, por lo tanto se está desperdiciado el 38% del material de producción y horas de trabajo remunerado.
UNIDAD 2 PROBABILIDAD.
Regla de Probabilidad. En un espacio muestral que contiene puntos muéstrales que son igualmente probables de ocurrir; la probabilidad P (A) de un evento A, es la razón del número de puntos que satisfacen la definición del evento A; n(A) con respecto al número de puntos muéstrales que hay en todo el espacio muestral; n(S). Es decir.
P(A)=\frac{n(A)}{n(S)}
Esta definición sólo es válida para eventos simples (cada uno de los posibles resultados individuales de un experimento) y cuando todos los resultados tienen la misma posibilidad de ocurrir.
De acuerdo a la definición de la probabilidad clásica, el fundamento para el cálculo de probabilidades es el conocimiento del espacio muestreal, lo cual no es siempre posible; sin embargo existen algunas técnicas y procedimientos para aproximarnos a su solución.
Ejemplos:
N°1.– Lanzamos un dado y observamos la cara superior.
El espacio muestral su resultado es el conjunto: S=\{1,2,3,4,5,6\}.
N°2.- Si lanzamos una moneda dos veces y se observa la cara superior.
El espacio muestral son las caras de la moneda al caer, mismas que pueden ser:
E={aa,as,sa, ss}.
N°3.– Si lanzamos un par de dados y observamos el número de puntos en cada uno.
S={(1,1)(1,2)(1,3)(1,4)(1,5)(1,6) (2,1)(2,2)(2,3)(2,4)(2,5)(2,6) (3,1)(3,2)(3,3)(3,4)(3,5)(3,6) (4,1)(4,2)}.
N°4.- Apoyados en el campo muestral del ejercicio anterior encontrar lo siguiente:
a) Los dados muestran el mismo valor.
b) El primer dado es el doble del segundo.
c) La suma es dos.
d) La suma es un número primo.
La solución es:
a) A =\{ (1,1)(2,2)(3,3)(4,4)(5,5)(6,6)\}
b) B = \{(2,1)(4,2)(6,3)\}
c) C = \{ 1,1\}
d) D = \{(1,1)(2,1)(1,2)(3,2)(2,3)(3,4)(4,3)(2,5)(5,2)(6,5)(5,6)(4,1)(1,4)(6,1)(1,6)\}
N° 5.-Si se lanzan 2 dados, ¿cuál será la probabilidad de que la suma de las caras que quedan hacia arriba sean de: a) 6; b) 9 y c) 11.

a) P(6)=\frac{5}{36} ó 13.89%
b) P(9)=\frac{4}{36}=\frac{1}{9} ó 11.11%
c) P(11)=\frac{2}{36} \frac{1}{18} ó 5.56%
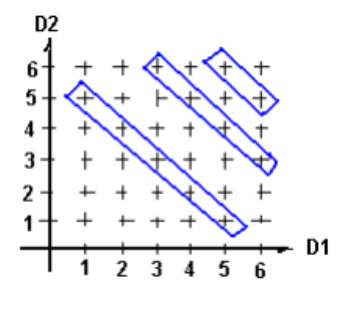
N°6.- ¿Cuál es la probabilidad de obtener 2 águilas y un sol, al lanzar tres veces una moneda?
Nos ayudamos por medio de un diagrama de árbol:

P(2A y S )= \frac{n(A)}{n(S)} = \frac{3}{8} ó 37.50%
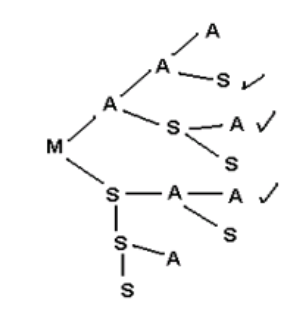
N°7.- Una caja contiene tres canicas; una roja, una blanca y una verde. Dos de ellas se extraen con reemplazamiento, es decir, una vez que se ha elegido una canica se observa su color y luego vuelve a introducirse en la caja, las canicas son revueltas antes de extraer una segunda canica y observar su color.
a) ¿Cuál es la probabilidad de que las canicas extraídas sea una verde y una blanca?

n(V y B)=2 \therefore P(V y B)= \frac{2}{9} ó 22.22%
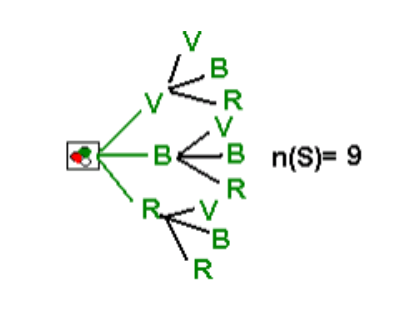
N° 8.- Si no hay reemplazamiento, ¿cuál será la probabilidad de que las canicas extraídas sean verdes y una blanca?
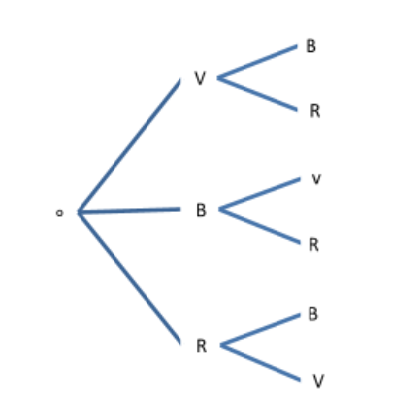

n(V y B)=2 \therefore P(V y B)= \frac{2}{6} = \frac{1}{3} ó 33.33%
Técnicas de Conteo.
Las técnicas de conteo se usan para encontrar el número de resultados posibles de que suceda un evento, cuando es difícil controlarlos mediante diagramas de árbol o por ser muy grande el número de posibilidades.
Principio Fundamental. Si una decisión, operación o acción puede tomarse de n1 formas diferentes y si después que ha sido efectuada, una de estas formas, una segunda decisión puede tomarse de n2 formas distintas, y una tercera acción puede tomarse de n3 formas distintas, entonces el número total de acciones o decisiones que puedan formarse será igual a n1 n2 n3…….nm que es lo que se conoce como Principio Fundamental de Conteo.
Ejemplos.
N°1.- Un estudiante tiene que seleccionar una de las cuatro materias optativas; una actividad extraescolar de entre danza, teatro, música y guitarra, y entre uno de los siguientes idiomas; inglés, francés e italiano. ¿Cuántas maneras distintas tiene que escoger?
(4)(4)(3) = 48 maneras diferentes.
N°2.- Una placa de automóvil en el D. F., consta de cuatro dígitos y tres letras.
a) ¿Cuántas placas se pueden hacer sin restricción?
b) Si la primera letra puede ser A, B, C, D, E, F y el primer dígito diferente de cero.
c) ¿Cuántas, si letras y números deben ser diferentes y la primera letra sólo puede ser la A?
Dígitos
a) (10)(10)(10)(10)
b) (9)(10)(10)(10)
c) (10)(9)(8)(7)
letras
(26) (26) (26) \rightarrow 175760000 placas diferentes
(6) (26) (26) \rightarrow 36504000 placas diferentes
(1) (25) (24) \rightarrow 3024000 placas diferentes
N°3.- Calcula el número posible de resultados en partidos que puede haber al llenar una boleta de pronósticos deportivos, si hay trece partidos y en cada uno hay tres opciones de ganar, empatar o perder.
n_1=(3)(3)(3)(3)(3)(3)(3)(3)(3)(3)(3)(3)(3) = 3^{13} = 1594323 opciones.
N°4.- En un estudio médico, los pacientes se clasifican en formas diferentes, de acuerdo a su tipo de sangre: AB+, AB-, A+, A-, B+, B-, y su presión sanguínea (baja, normal y alta) ¿ Cuál es el número de formas posibles para clasificar un paciente?
(6)(3)= 18 = 1594323 Formas de clasificar a un paciente.
N°5.– Si no se permiten repeticiones: a) ¿Cuántos números de tres dígitos se pueden formar con los siguientes seis: 2, 3, 5, 6, 7, 9? b) ¿Cuántos son pares? c) ¿Cuántos son impares? d) ¿Cuántos son múltiplos de 5?
a) 654 = 120 números
b) 542 = 40 números pares
c) 544 = 80 números nones
d) 541 = 20 números múltiplos de cinco.
N°6.- ¿Cuántos números de tres dígitos se pueden formar con 0, 1, 2, 3, 4, 5, y 6 si ninguno puede repetirse ¿ b) Cuántos de estos son pares? c) ¿Cuántos son mayores de 400?
a) (6)(6)(5) = 180 números
b) (6)(5)(1) = 30 números terminados en cero
(5)(6)(3) = 90 números pares
=120 totales de números pares
c) (3)(6)(5) = 90 números mayores de 400.
PRINCIPIO ADITIVO.
Si se desea llevar a efecto una actividad, la cual tiene formas alternativas para ser realizada, donde la primera de esas alternativas puede ser realizada de M maneras o formas, la segunda alternativa puede realizarse de N maneras o formas… y la última de las alternativas puede ser realizada de W maneras o formas, entonces esa actividad puede ser llevada a cabo de:
M + N +…+ Wmaneras o formas.
Ejemplos:
N° 1.- Una persona desea comprar una lavadora de ropa, para lo cual ha pensado que puede seleccionar de entre las marcas Whirpool, Easy y General Electric, cuando acude a hacer la compra se encuentra que la lavadora de la marca W se presenta en dos tipos de carga ( 8 u 11 kilogramos), en cuatro colores diferentes y puede ser automática o semiautomática, mientras que la lavadora de la marca E, se presenta en tres tipos de carga (8, 11 o 15 kilogramos), en dos colores diferentes y puede ser automática o semiautomática y la lavadora de la marca GE, se presenta en solo un tipo de carga, que es de 11 kilogramos, dos colores diferentes y solo hay semiautomática. ¿Cuántas maneras tiene esta persona de comprar una lavadora?
Solución:
M = Número de maneras de seleccionar una lavadora Whirpool
N = Número de maneras de seleccionar una lavadora de la marca Easy
W = Número de maneras de seleccionar una lavadora de la marca General Electric
M = 2 x 4 x 2 = 16 maneras
N = 3 x 2 x 2 = 12 maneras
GE = 1 x 2 x 1 = 2 maneras
M + N + GE = 16 + 12 + 2 = 30 maneras de seleccionar una lavadora.
N°2.- Rafael Luna desea ir a las Vegas o a Disneylandia en las próximas vacaciones de verano, para ir a las Vegas él tiene tres medios de transporte para ir de Chihuahua al Paso Texas y dos medios de transporte para ir del Paso a las Vegas, mientras que para ir del paso a Disneylandia él tiene cuatro diferentes medios de transporte, a) ¿Cuántas maneras diferentes tiene Rafael de ir a las Vegas o a Disneylandia?, b) ¿Cuántas maneras tiene Rafael de ir a las Vegas o a Disneylandia en un viaje redondo, si no se regresa en el mismo medio de transporte en que se fue?
Solución:
a) V = maneras de ir a las Vegas
D = maneras de ir a Disneylandia
V = 3 x 2 = 6 maneras
D = 3 x 4 = 12 maneras
V + D = 6 + 12 = 18 maneras de ir a las Vegas o a Disneylandia
b) V = maneras de ir y regresar a las Vegas
D = maneras de ir y regresar a Disneylandia
V = 3 x 2 x 1 x 2 = 12 maneras
D = 3 x 4 x 3 x 2 = 72 maneras
V + D = 12 + 72 = 84 maneras de ir a las Vegas o a Disneylandia en un viaje redondo
¿Cómo podemos distinguir cuándo hacer uso del principio multiplicativo y cuando del aditivo?
Es muy simple, cuando se trata de una sola actividad, la cual requiere para ser llevada a efecto de una serie de pasos, entonces haremos uso del principio multiplicativo y si la actividad a desarrollar o a ser efectuada tiene alternativas para ser llevada a cabo, haremos uso del principio aditivo.
Retomando la definición clásica de la probabilidad, representada por la fórmula
P(A) = \cfrac{ \# \text {de casos favorables de A}}{ \# \text{ de casos posibles}}
EJEMPLO 1
Se realiza el lanzamiento de un dado, determine lo siguiente:
1. ¿Cuál es la probabilidad de obtener un tres?
2. ¿Cuál es la probabilidad de obtener un número par?
3.¿Cuál es la probabilidad de obtener un número primo?
SOLUCIÓN
1.Suceso T = “obtener un tres”. T = {3}. Luego, la probabilidad de obtener un tres será:
P(T)=\cfrac{\text{cantidad de tres}}{\text{número de caras del dado}}= \cfrac{1}{6}= 0.1666 \thickapprox 0.5 ó 50%
2. Suceso P = “sacar un número par”. P = {2, 4 ,6}. Luego, la probabilidad de obtener un número par será:
P(P)=\cfrac{\text{numeros pares }}{\text{número de caras del dado}}= \cfrac{3}{6}= \cfrac{1}{2}= 0.1666 \thickapprox 0.17 ó 17%
3. Suceso Pr = “sacar un número primo”. Pr = {1, 2, 3, 5}. Luego, la probabilidad de obtener un número primo será:
P(Pr)=\frac{\text{numeros primos }}{\text{numero de caras del dado}}= \cfrac{4}{6}= \cfrac{2}{3}= 0.6666 \thickapprox 0.67 ó 67%
EJEMPLO 2
En una baraja de 40 cartas, si se extrae una. a) ¿Cuál es la probabilidad de sacar un AS?; y b) ¿Sea una de ESPADA?
SOLUCIÓN:
a) Suceso A = “extraer un As”. Luego, la probabilidad de extraer un As será:
P(Pr)=\cfrac{\text{cantidad de Ases }}{\text{número total de cartas}}= \cfrac{4}{40}= \cfrac{1}{10}= 0.1 ó 10%
b) Suceso E = “extraer una de Espadas”. Luego, la probabilidad de extraer una de Espadas será:
P(Pr)=\cfrac{\text{cantidad de Espadas }}{\text{número total de cartas}}= \cfrac{4}{10}= \cfrac{1}{4}= 0.25 ó 25%
REGLA DE LA SUMA DE PROBABILIDADES (PROBABILIDAD DE UNIÓN)
Sean A y B dos sucesos cualesquiera, entonces, la probabilidad de ocurrencia de los sucesos A o B, se conoce como la probabilidad de unión y se denota P(A U B) y su valor se determina mediante la expresión:
P(A\cup B)=P(A)+P(B)-P(A\cap B)
Si A y B son sucesos incompatibles (que no tienen nada en común) entonces:
P(A\cup B)=P(A)+P(B)
Corolario: Sean A_1, A_2, A_3,…, A_n sucesos incompatibles entre sí, entonces, la probabilidad de unión de ellos será:
P(A_1\cup A_2 \cup A_3 \cup ...\cup A_n)=P(A_1)+P(A_2)+P(A_3)+...P(A_n)
EJEMPLO 1
Los alumnos de Laboratorio de Biología tienen que realizar dos pruebas, una teórica y otra práctica. La probabilidad de que un estudiante apruebe la parte teórica es de 0.6, la probabilidad de que apruebe la parte práctica es de 0.8 y la probabilidad de que apruebe ambas pruebas es 0.5.
1. ¿Cuál es la probabilidad de que un alumno no apruebe ninguno de los dos exámenes?
2. ¿Cuál es la probabilidad de que un alumno apruebe solamente uno de los dos exámenes?
SOLUCIÓN:
Se definen los sucesos:
a) Suceso T ∩ P = “ ni TEORÍA ni PRACTICA”. Luego, la probabilidad de no aprobar ni teoría ni práctica será:
pero, PT ∩ P=1-PT ∪P
entonces, PT ∪P=PT+PP-PT ∩P ,
por lo tanto, PT ∪P=0.6+0.8-0.5=0.9
b) Suceso T ∩P = “aprobar solo teoría”, luego, la probabilidad de aprobar solo teoría será:
P(T \cap P)=P(T)-P(T \cap P)=0.6-0.5=0.1 o 10%
Suceso T∩P = “aprobar solo practica”, luego, la probabilidad de aprobar solo practica será:
P(T \cap P)=P(P)-P(T \cap P)=0.8-0.5=0.3 o 30%
entonces, la probabilidad de aprobar “solo una” se refiere a aprobar solo la teoría o solo la práctica. Al ser sucesos incompatibles entonces la probabilidad de unión se calcula por:
P(T \cap P \cup T \cap P)=P(T \cap P)+P(T \cap P)=0.1+0.3=0.4 o 40%
EJEMPLO 2
En cierta habitación de hospital la probabilidad de que un paciente sea ingresado con problemas de presión arterial es de 0,7; la probabilidad de que ingrese con problemas renales es 0,5 y la de que ingrese con ambos problemas es de 0,3. Hallar:
1. La probabilidad de que un paciente ingrese con al menos una de las dos patologías.
2. La probabilidad de que no presente ninguna de las dos patologías.
3. La probabilidad de que ingrese con problemas renales y sin problemas de presión arterial.
SOLUCIÓN:
Se definen los sucesos:
Suceso P: paciente que ingresa con problemas de presión arterial
Suceso: paciente que ingresa con problemas renales
a) La probabilidad que un paciente ingrese con al menos una de las dos patologías es que ingrese con problemas renales o con problemas de presión arterial, lo que se denota como:
P(P \cup R) =P(P)+P(R)-P(P \cap R)=0.7+0.5-0.3=0.9 o 90%
b) La probabilidad que sea ingresado con otra patología que no sea ni presión arterial ni renal viene a ser el complemento de que ingrese con alguna de las dos. Por lo tanto, esta probabilidad será:
P(\overline{P} \cap \overline{R}) =1-P(P \cup R)=1-0.9=0.1 ó 10%
c) Esta puede entenderse como la probabilidad de que sea ingresado solo con problemas renales, entonces:
P(R \cap \overline{P}) =P(R)- P(R \cap P)=0.5-0.3=0.2 ó 20%
EJEMPLO 3
Suponga que el 70% de los crímenes ocurren de noche y que la probabilidad de ser asaltado, golpeado y de día es 0,2; mientras que de un total de 6528 asaltos 3798 se llevaron a cabo con violencia.
1. ¿Cuál es la probabilidad de seleccionar al azar una persona asaltada, golpeada y de noche?
2. ¿Cuál es la probabilidad de seleccionar a una persona asaltada sin violencia?
SOLUCIÓN:
Se definen los sucesos:
Suceso V: crimen con violencia
Suceso D: crimen de día
Suceso N: crimen de noche
Para la resolución de este problema debemos hacer una combinación de las formas de calcular las probabilidades de ocurrencia, puesto que tenemos algunos datos en frecuencia relativa y otros en frecuencia absoluta. Para esos datos, debemos utilizar la fórmula de la probabilidad clásica.
El 70% de los crímenes ocurren de noche, entonces, P(N)= 0,7; por tanto, P(D) = 0,3
Si 3798 crímenes se cometieron con violencia, entonces 2730 ocurrieron sin violencia
Entonces:
P(V) =\cfrac{\text{cantidad de crimenes con violencia}}{\text{número de crimenes}}=\cfrac{3798}{6528}=0.58 ó 58%
Por último,
P(V \cup D)= 0.2
Con estos datos se procede a determinar los valores de probabilidades
a) La probabilidad de que una persona de asaltada, golpeada y de noche se puede entender como “con violencia y de noche”. Entonces, se sabe que:
P(V \cap N)+P(V \cap D)=P(V) \Longrightarrow P(V \cap N)=P(V)-P(V \cap D)
P(V \cap N)=P(V)-P(V \cap D)= \Longrightarrow P(V \cap N)= 0.58-0.2=0.38
P(V)=\cfrac{\text{cantidad de crimenes sin violencia}}{\text{número de crímenes }}=\cfrac{2730}{6528}=0.42 ó 42%
COMBINACIONES Y PERMUTACIONES
Normalmente usamos la palabra “combinación” descuidadamente, sin pensar en si el orden de las cosas es importante. En otras palabras:
“Mi ensalada de frutas es una combinación de manzanas, uvas y bananas”: no importa en qué orden pusimos las frutas, podría ser “bananas, uvas y manzanas” o “uvas, manzanas y bananas”, es la misma ensalada.
La combinación de una cerradura es 472″: ahora sí importa el orden. “724” no funcionaría, ni “247”. Tiene que ser exactamente 4-7-2.
Así que en matemáticas usamos un lenguaje más preciso:
Si el orden no importa, es una combinación.
Si el orden sí importa es una permutación.
Con otras palabras:
Permutaciones. Una permutación es una combinación ordenada.Permutaciones. Una permutación es una forma en la que pueden presentarse los objetos o eventos, y en la cual el orden de aparición es muy importante.
Permutaciones de “n” objetos tomados de “r” _n P_r=\frac{n!}{(n-r)!}
En dónde; n es el número total de objetos o eventos y, r el número de objetos que se desea considerar y puede ser desde 1 hasta n.
Ejemplos.
N°1.- Los tres dígitos 2, 5 y 8 pueden formar los números 258, 285, 528, 582, 825 y 852. Cada uno de ellos es una permutación de los dígitos 2, 5 y 8, y refleja valores muy importantes entre sí.
N°2.- Las letras A, V, E; forman: AVE, AEV, VAE, VEA, EAV y EVA. Son palabras diferentes.
Existen siete casos en las que pueden operarse las permutaciones.
Primero. Permutar algunos objetos de todos diferentes.
Ejemplo:
N°3.- En una caja hay 4 canicas (Azul, Blanca, Verde y Gris) si se extraen de la caja dos de ellas, ¿en qué orden pueden aparecer?
_4 P_2=\cfrac{4!}{(4-2)!}=\cfrac{4.3.2!}{(2)!}=12
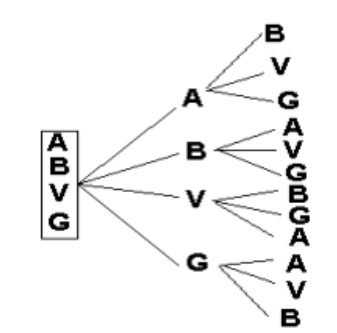

(A,B), (A,V), (A,G)
Segundo. Permutar todos los objetos, de todos diferentes.
N°4.- En una caja hay un billete de $100.00, otro de $50.00 y uno más de $20.00. Tres personas van a tomar cada uno un billete, sin ver. Determine las formas en que pueden distribuirse los billetes.
_3 p_3=\cfrac{3!}{(3-3)!}=\cfrac{3.2.1!}{1!}=6
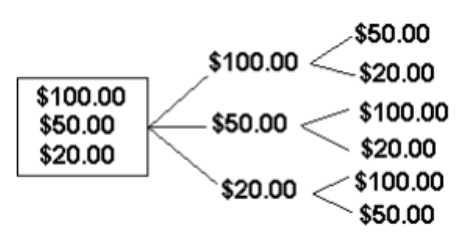

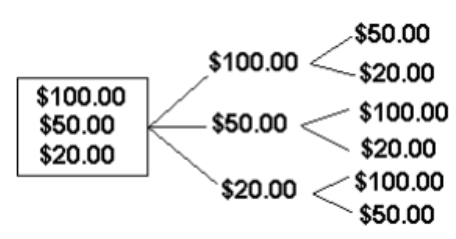

P = (100. 50)(100,20)
Tercero. Permutar todos los objetos, de algunos repetidos.
P=\cfrac{(k_1+k_2+...+k_n)!}{k_1!k_2!...k_n!} Formas
N°5.- En una caja hay 2 canicas azules y 5 verdes. Si se extraen una por una de la caja, ¿en qué orden pueden aparecer?
P=\cfrac{(2+5)!}{2! 5!}=\cfrac{5040}{240}=21
Cuarto. Permutar algunos objetos, de algunos repetidos. No existe una fórmula fácil para determinar el número de permutaciones cuando se toman algunos objetos de un conjunto que contiene varios artículos iguales entre sí.
N°6.– En una caja hay 2 canicas azules y 5 verdes. Si se extraen 4 de ellas de la caja, ¿en qué orden pueden aparecer?
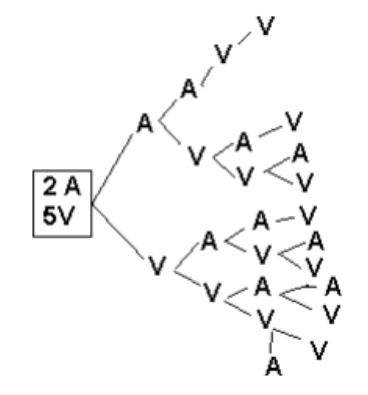

Quinto. Permutar con reemplazo. Esto es cuando el número de objetos sea limitado, pero el número de veces que se presenten sea infinito, cuando los objetos seleccionados pueden ser elegidos de nuevo. En las permutaciones anteriores, el número de objetos estaba perfectamente definido (4 canicas, 3 billetes, etc.). La diferencia entre una y otra se conoce como reemplazo:
P= n^m Forman Formas
N°7.- Los resultados posibles de un juego son perder o ganar. Si se juegan 4 juegos, ¿cuáles son los resultados posibles?
Lista

P= n^m=2^4=16
Sexto. Permutar con Repetición. Con frecuencia se encuentran conjuntos de objetos iguales, si queremos saber el número de permutaciones, la fórmula está dada por.
P=\cfrac{n!}{n_1! \cdot n_2! \cdot n_3! \cdot ... n_r!} ; Donde n_1 son iguales, …. n_2 son iguales …. n_r son iguales.
N°8.- ¿Cuántas palabras diferentes se pueden formar con la palabra “ESTADÍSTICA”?
P=\cfrac{11!}{2! \cdot 2! \cdot 2! \cdot 2!}=2 494 800
Séptimo. Permutación Circular. Toda permutación de “n” objetos en la que el sucesor del último es el primero, se llama permutaciones circulares y está dada por la expresión. P = (n −1)!
N°9.- ¿De cuántas maneras se puede acomodar doce personas en una mesa circular?
P = (12 −1)! = 39916800.
Ejercicios:
1.- En una carrera de autos hay nueve participantes. ¿De cuántas maneras es posible la clasificación final?
P_9=9!=362880 maneras de clasificación posibles.
2.- ¿Cuántos números distintos se pueden escribir con los dígitos 1 y 5 en que el 1 se repite 2 veces, el 5 se repite 3 veces?
- Intervienen todos los elementos.
- Se pueden repetir.
- Influye el orden en el que se coloca.


3.- ¿Cuántos números diferentes pueden formarse con las cifras del número 458870?
Tenemos seis elementos, de los cuales uno de ellos se repite dos veces. Influye el orden, ya que son n{umeros e intervienen todos los elementos. Como se repite una de las cifras, hablamos de permutaciones con repetición de una cifra dos veces.
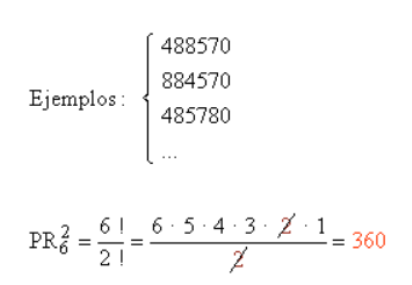
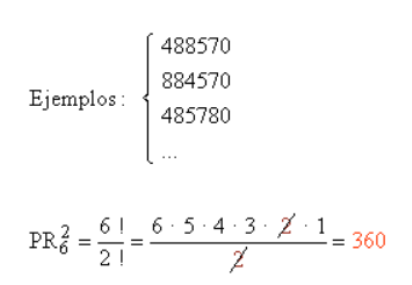
4.- ¿De cuántas formas se pueden sentar 4 personas A, B, C y D en una mesa circular?
en un principio, podríamos pensar que son permutaciones de 4 elementos P_4 = 24 formas. Sin embargo en el dibujo vemos que :
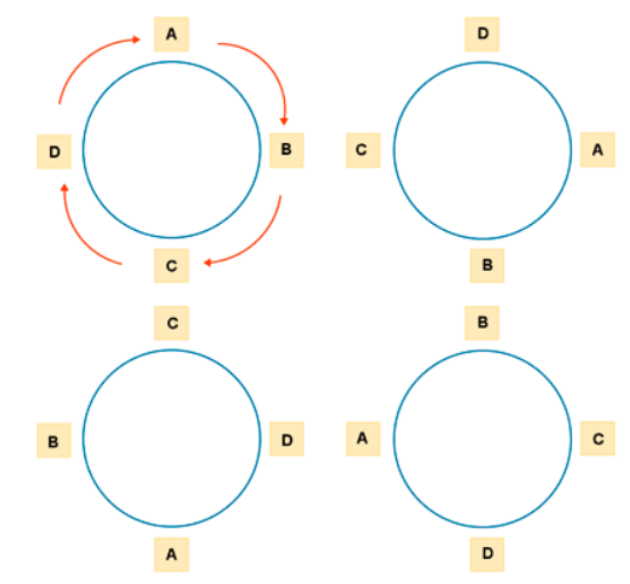

Esas 4 posiciones son la misma, ya que cada persona tiene a la izquierda, a la derecha y al frente a la misma persona
P_{C4} = (4-1)! = 3! = 3 \cdot 2
5.- Un estudiante presenta un examen de 20 preguntas de verdadero – falso. ¿Cuántas maneras existen para resolver el examen
P = n^m = c^{20}=1048576
6.- Hay ocho trabajadores limpiando una casa grande. Para limpiar las ventanas se necesitan cinco, para las alfombras se necesitan dos, y uno para el resto de la casa. ¿De cuantas formas distintas se pueden asignar las tareas a los ocho trabajadores?
P_8^{5,2,1}= \cfrac{8!}{5!2!1!}=\cfrac{8 \cdot 7 \cdot \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{5! 2! 1!}= 168 formas
7.- ¿De cuántos modos pueden sentarse un padre, su esposa y cuatro hijos en un mesa redonda, cuando siempre a partir del padre?
P_{cir}^n= (n-1)! = P_{cir}^6=(6-1)! =5! = 120 modos
8.-Doce estudiantes van a ir a Veracruz en tres carros, 3 en el carro # 1, cuatro en el carro # 2 y cinco en el carro # 3. ¿De cuántas formas se pueden acomodar si cualquiera puede conducir?
P_{12}^{3,4,5}= \cfrac{12!}{3!4!5!}= 27720 modos
9.- El presidente, vicepresidente, secretario y tesorero de una determinada asociación, se elegirán de entre 10 candidatos, encontrar el número de maneras distintas en que estos pueden ocuparse.
P_{4}^{10}= \cfrac{10!}{(10-4)!}= 5040 maneras de ocupar
10.- ¿ De cuántas formas diferentes se pueden colocar 6 llaves en un llavero en forma de aro?.
P_{cir}^{n}= (n-1)! = P_{cir}^{6}=(6-1)!=5!=120 formas
11.- Un testigo del robo de un Banco dijo que el número de la placa del automóvil de los ladrones era un número de seis dígitos, de los cuales los tres primeros eran 487. No recordó los últimos tres dígitos, pero estaba totalmente seguro que éstos eran diferentes de los tres primeros ¿Cuántos números de placas de automóvil tendrán que investigar la policía?
P_{7}^{3}= \cfrac{7!}{(7-3)!}=210 números
12.- ¿De cuántas maneras 3 americanos, 4 franceses, 4 daneses y 2 italianos pueden sentarse en una fila de modo que los de la misma nacionalidad se sienten juntos?
Como no especifica que nacionalidad va primero habrá P4 para las nacionalidades y P3 para los americanos, P4 para los franceses, P4 para los daneses y P2 para los italianos
P_{4} \cdot P_{3} \cdot P_{4} \cdot P_{4} \cdot P_{2} = 4! \cdot 3! \cdot 4! \cdot 4! \cdot 2! = 165888 números
13.- En un tren hay asiento para 4 personas. En cierta estación se suben 8 personas. ¿De cuántas maneras pueden ocupar los lugares?
P_{4}^{8}= \cfrac{8!}{(8-4)!}=1680 formas
14.- ¿De cuántas maneras pueden colocar en hilera 12 libros distintos: a) Cuándo un libro dado debe ocupar un extremo especifico?, b) Cuándo un libro dado debe ocupar uno de los extremos? c) Cuándo un determinado par de libros deben quedar uno al lado de otro?
a) 11!=39 916 800 formas
b) 2! \cdot 11!= 79 833 600 formas
c) 11! \cdot 2! = 79 833 600 formas
15.- ¿De cuántas maneras pueden acomodarse tres libros diferentes de química y cuatro diferentes de física en un librero, de manera que los libros de química queden siempre juntos?
P_3\cdot P_4=3! \cdot 4!=144 maneras
16.- ¿Cuántas señales diferentes, cada una de 9 banderas colgadas en una línea vertical, pueden formarse con 4 banderas amarillas idénticas, 3 banderas rojas idénticas y 2 banderas azules idénticas?
P_{4,3,2^9}= \cfrac{9!}{4! \cdot 3! \cdot 2!}= 1260 señales
17.- ¿De cuántas maneras se puede acomodar una reunión de 13 personas alrededor de una mesa?
P_{c}= (n-1)! = (13-1)! = 479 001 600 señales
18.- ¿De cuantas formas 4 niños y 4 niñas se pueden sentar en una banca alternadamente?
Por sexo se pueden sentar P_2 =2!=2
Los niños se pueden sentar P_4= 4!=24
Las niñas se pueden sentar P_4=4! = 24
P_t=2 \cdot 24 \cdot 24=1152 formas
19.- En una carrera de 400 metros participan 10 atletas. ¿De cuántas formas distintas podrán ser premiados los tres primeros lugares con medalla de oro , plata y bronce?
Solución:
Método 1: Empleando el principio fundamental de conteo
10 x 9 x 8 = 720 maneras
Método 2: (usando la fórmula de permutación lineal)
* Se busca las diferentes ternas (r = 3) que se pueden formar con los 10 atletas (n = 10)
P_3^{10}= \cfrac{10!}{7!}=\cfrac{7!x8x9x10}{7!}=720
20.- Con las letras de la palabra libro, ¿cuántas ordenaciones distintas se pueden hacer que empiecen por vocal?
La palabra empieza por i , o seguida de las 4 letras restantes tomadas de 4 en 4.
Sí entran todos los elementos. Sí importa el orden. No se repiten los elementos.
P_2 \cdot P_4 = 2 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 48
21.- a) ¿De cuántas maneras pueden formarse 6 personas para subir a un autobús? b) Si 3 de ellas insisten en estas juntas. c) Si dos personas no pueden estar juntas porque no se toleran ¿cuántas alternativas habría para estar separadas?
a) P_6=6! = 720 formas.
b) P_3 \cdot P3=3! \cdot 3!=6 \cdot 6=36 formas.
c) P_2 \cdot 4 \cdot 5 \cdot 3 \cdot 2 = 240 formas
22.- Si una urna contiene 10 bolas, determinar el número de pruebas ordenadas de tamaño 4. a) Con sustitución. b) Sin sustitución.
a) P = 10^4= 10 000 formas.
b) P_r^n= P_4^{10}= \cfrac{10!}{n-r}!=5 040 formas.
23.- ¿Cuántas líneas rectas se pueden trazar pasando por ocho puntos, de los cuales no hay cinco que estén sobre la misma recta?
P_8^{5,3}= \cfrac{8!}{5!\cdot 3!}=56 líneas
COMBINACIONES
aUna combinación es una forma en la que pueden presentarse los objetos o eventos, y en la cual el orden de aparición no importa. La multiplicación de los dígitos 2, 5 y 8 puede hacerse de muchas formas diferentes. 2 \cdot 5 \cdot 8, 2 \cdot 8 \cdot 5, 5 \cdot 2 \cdot 8, etc., pero en todos los casos el resultado será el mismo.
Permutaciones de “n” objetos tomados de “r” en “r” = _n C_r =\cfrac{n!}{r!*(n-r)!}
En dónde; n es el número total de objetos o eventos y, r el número de objetos que se desea considerar.
Nota. Para cualquier pareja de números enteros positivos “n” y “r”, exceptuando r = 1. El número de permutaciones es mayor que el número de combinaciones.
Ejemplos.
N°1.- Hay un grupo de cinco personas, las que pueden identificarse con las letras A, B, C, D y E. De ellas se van a seleccionar tres para una misión especial. ¿De cuántas formas diferentes se pueden seleccionar las tres personas?
_5C_3 =\cfrac{5!}{3!(5-3)!}=\cfrac{5 \cdot 4 \cdot 3!}{3! 2}=10

N°2.- Una preselección de fútbol está formada por 25 jugadores. ¿De cuántas formas diferentes puede el entrenador integrar un equipo de 11 jugadores?
_{25}C_{11} =\cfrac{25!}{11!(25-11)!}=
\frac{25 \cdot 24 \cdot 23 \cdot 22\cdot 21\cdot 20 \cdot 19 \cdot 18 \cdot 17 \cdot 16 \cdot 15 \cdot 14!}{11 \cdot 10\cdot 9\cdot 8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2 \cdot 14!}
=\cfrac{5 \cdot 23 \cdot 2 \cdot 19 \cdot 2 \cdot 17 \cdot 2 \cdot 15 \cdot 14!}{14!} = 4 457 400
N°3.- Calcular la probabilidad de obtener una flor (5 del mismo palo sin ser consecutivas), en una mano de 5 naipes, tomados de una baraja de 52 cartas.
{52}C{5} =\cfrac{52!}{5!(52-5)!}= \cfrac{52 \cdot 51 \cdot 50 \cdot 49 \cdot 48 \cdot 47!}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 47!} = 2598960
{13}C{5} = \cfrac{13!}{5!(13-5)!}= \cfrac{13 \cdot 12 \cdot 11 \cdot 10 \cdot 9 \cdot 8!}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 8!} = \cfrac{13 \cdot 11 \cdot 9 \cdot 8!}{8!}= 1287
P(5E)=\cfrac{ _{13}C_5}{ _{52}C_5}=\cfrac{1287}{2598960}=4.95X10^{-4}=0.0005 ó 0.05%
Multiplicación de Combinaciones. Esto sucede en las combinaciones y es una forma de lo más común, en la cual es necesario multiplicar los resultados parciales de dos o más combinaciones.
N°4.- De un total de 5 hombres y 4 mujeres se va a formar un comité de 3 hombres y 2 mujeres. ¿De cuántas formas puede quedar integrado?
_5C_3=\cfrac{5!}{3!(5-3)}=\cfrac{5\cdot 4 \cdot 3! }{2\cdot 3!}=10
_4C_2=\cfrac{4!}{2!(4-2)!}=\cfrac{4 \cdot 3 \cdot 2!}{2 \cdot 2!}=6 Formas = (10)(6)=60
N°5.- Si de un estante tomamos 2 de 3 libros, ¿Cuántas combinaciones pueden realizarse?
_3C_2=\cfrac{3!}{(3-2)!2!}=\cfrac{3!}{1! 2!}=\cfrac{6}{2}=3


Por lo tanto, el resultado se reduce a 3 posibles formas ya que en una combinación el orden de los elementos no es importante.
N°6.- En una prueba de atletismo en la que participan 8 atletas se pueden clasificar sólo 3 para la final.
¿Cuantos grupos distintos de finalistas se pueden formar?
Solución:
El orden no importa. Luego son combinaciones. Los elementos no se pueden repetir. Entonces tenemos combinaciones sin repetición, de 8 elementos tomados de 3 en tres:
C_{8,3}=\cfrac{8}{3}=\cfrac{8!}{3!(8-3)!}=\cfrac{8 \cdot 7 \cdot \cancel{6} \cdot \cancel{5!} }{\cancel{3!} \cdot \cancel{5!}}=3
N°7.- Un estudiante que realiza un examen debe responder 7 de las 10 preguntas. El orden no importa. ¿De cuántas formas puede responder el examen?
Existen C_{7}^{10}=\cfrac{10!}{(10-7)!7!}=120 combinaciones posibles de preguntas que puede contestar.
N°8.- Juan quiere dar una fiesta para algunos de sus amigos. Debido al tamaño de su casa, sólo puede invitar a 11 de sus 20 amigos. ¿De cuántas formas puede seleccionar a los invitados?
Hay C_{11}^{20}=\cfrac{20!}{(20-11)!}=167 960 formas de elegir a los 11 amigos.
N°9.– En una reunión de 6 personas, ¿cuántos saludos de mano pueden intercambiarse, si entre cada 2 personas, se dan la mano una sola vez?
C_{2}^6=\cfrac{6!}{(6-2)!}=15 saludos
N°10.- ¿Cuántas manos diferentes le pueden tocar a un jugador de poker?
Una mano de poker es de 5 cartas y la baraja inglesa consta de 52; por ende, en cada mano se obtiene, de una en una, la muestra de 5 cartas distintas; para efectos de conteo, a esta manera de tomar la muestra se le denomina muestreo sin reemplazamiento. La primera carta puede ser cualquiera de la 52, la segunda puede ser cualquiera de las 51 restantes,…, y la quinta, que puede ser cualquiera de las 48 que quedan. El orden en el que salen las cartas no importa y evidentemente no se permite la repetición; por lo tanto, son combinaciones de 52 objetos tomados de 5 en 5.
C_{52}^5=\cfrac{52!}{5! 47!}=\cfrac{52x51x50x49x48x\cancel{47}!}{5x4x3x2x1x\cancel{47}!}= \cfrac{311´875,200}{120}=2´598,960
N°11.- Si en el grupo 20 de “Probabilidad” hay 14 estudiantes mujeres, ¿cuántos partidos diferentes de voleibol se podrían realizar, si cada equipo es de 6 jugadoras?
Es necesario considerar la conformación de dos equipos: El primer equipo se puede formar de 6C14 maneras, pues se pueden elegir 6 jugadoras diferentes de entre 14 disponibles; el segundo equipo se puede formar de 6C8 maneras, pues ahora se eligen 6 jugadoras de entre las 8 mujeres que quedan disponibles. El producto de estas dos combinaciones, invocando el principio fundamental del conteo, proporciona el número de partidos que pueden realizarse, pero cada uno de ellos está considerado dos veces, pues una misma sexteta puede pertenecer a ambas combinaciones; el problema se resuelve dividiendo el producto de las dos combinaciones, entré las permutaciones de los 2 equipos:
\cfrac{ C_{14}^6 C_{8}^6}{P_2}=\cfrac{1}{2!} \cfrac{14!}{6!8!} \cfrac{8!}{6!2!}=\cfrac{1}{2} \cfrac{2162160}{720} \cfrac{56}{2}=42, 042 partidos
N°12.- A una reunión acuden 10 personas. Si se saludan con apretones de manos entre ellos, ¿Cuántos apretones se producen?
Resolución:
Cada apretón es una combinación de 2 en 2 de las 10 personas.
\text{N° apretones}= C_2^{10}=\cfrac{10!}{2!8!}=\cfrac{9x10}{2}=45
N°13.- Uniendo 3 vértices de un hexágono regular, ¿Cuántos triángulos diferentes se obtienen?
Solución:
Cada triángulo se obtiene combinando 3 vértices de los 6 que tiene el hexágono.
\text{N° triángulos}= C_3^{6}=\cfrac{6!}{3!3!}=\cfrac{4x5x6}{1x2x3}=20
N° 14.- En una prueba de atletismo en la que participan 8 atletas se pueden clasificar sólo 3 para la final. ¿Cuantos grupos distintos de finalistas se pueden formar?
Solución:
El orden no importa. Luego son combinaciones. Los elementos no se pueden repetir. Entonces tenemos combinaciones sin repetición, de 8 elementos tomados de 3 en tres:
C_{8,3}=\displaystyle\binom{8}{3}=\cfrac{8!}{3!(8-3)}=\cfrac{8 \cdot 7 \cdot \cancel{6} \cdot 5!}{\cancel{3!} \cdot \cancel{5!}}=56
N°15.- ¿Cuántas combinaciones se pueden hacer con dos elementos tomados del conjunto C = {a,b,c,d,e,f} ? Escribe las combinaciones posibles.
Solución:
Tenemos que hallar el número de combinaciones del conjunto de seis elementos tomados de dos en dos:
C_{6,2}=\displaystyle\binom{6}{2}=\cfrac{6!}{2!(6-2)!}=\cfrac{6!}{2! \cdot 4!}=\cfrac{6 \cdot 5 \cancel{\cdot 4 \cdot 3 \cdot 2} \cdot 1}{2 \cdot 1 \cancel {\cdot 4 \cdot 3 \cdot 2} \cdot 1 }= 15
N°16.- Calcula el número de boletos de Lotería Primitiva que es necesario rellenar para que te toque el primer premio con toda probabilidad (Hay que acertar 6 números de un total de 49).
Solución:
Hay que calcular el número de grupos diferentes de 6 números de entre 49 diferentes. En otras palabras, tenemos que calcular las combinaciones de 49 elementos tomados de 6:
C_{49,6}=\displaystyle\binom{49}{6}=\cfrac{49!}{6!(49-6)!}=13983816
N°17.- En una clase de 35 alumnos se quiere elegir un comité formado por tres alumnos. ¿Cuántos comités diferentes se pueden formar?
No entran todos los elementos.
No importa el orden: Juan, Ana.
No se repiten los elementos.
C_{35}^3=\cfrac{35 \cdot 34 \cdot 34 \cdot 33}{3 \cdot 2 \cdot 1}=6545
N°18.- ¿De cuántas formas pueden mezclarse los siete colores del arcoiris tomándose de tres en tres?
No entran todos los elementos.
No importa el orden.
No se repiten los elementos.
C_7^3=\cfrac{7 \cdot \cancel{6} \cdot 5 }{\cancel{3 \cdot 2} }=35
N°19.– A una reunión asisten 10 personas y se intercambian saludos entre todos. ¿Cuántos saludos se han intercambiado?
No entran todos los elementos.
No importa el orden.
No se repiten los elementos.
C_{10}^2=\cfrac{10 \cdot 9 }{2}=45
N°20.– Se desea formar un comité de 7 seleccionados 4 físicos y 3 matemáticos de u grupo de 8 físicos y 6 matemáticos. ¿De cuántas maneras podrá seleccionarse?
1° Seleccionamos 4 físicos de 8, C_{4}^8=\cfrac{8! }{(8-4)!4!}=70 formas
2° Seleccionamos 3 matemáticos de 6, C_{3}^6=\cfrac{6! }{(6-3)!4!}=20 formas
Aplicando el principio de multiplicación C_{4}^8 x C_{4}^8 =70 x 20 = 1400 formas
N°21.- De un grupo de 5 estudiantes, cuántos grupos diferentes de tres alumnos podrían formarse.
C_{3}^5=\cfrac{5! }{(5-3)!3!}=10 grupos
N°22.- Con 7 sumandos diferentes ¿Cuántas sumas distintas de 4 sumandos se podrán efectuar?
C_{4}^7=\cfrac{7! }{(7-4)!4!}=35 sumas diferenciales
N°23.- Un grupo de 16 personas desean escoger entre sus miembros un comité de 3 personas que los represente. ¿De cuántas formas distintas se puede seleccionar dicho comité?
C_{3}^16=\cfrac{7! }{(7-3)!3!}=560 comites
N°24.- En un examen de matemáticas, un estudiante debe responder siete preguntas de las diez dadas. ¿De cuántas formas diferentes debe de seleccionar, si él debe responder por lo menos, tres de las cinco primeras preguntas
Solución
El estudiante puede responder tres de las cinco primeras preguntas y 4 de las últimas 5 preguntas; o cuatro de las cinco primeras preguntas y 3 de las últimas; o cinco de las primeras cinco y dos de las últimas. Como no interesa el orden se trata de una combinación, por lo tanto tenemos:
C_{3}^5 x C_{4}^5 + C_{4}^5 x C_{3}^5 + C_{5}^5 x C_{2}^5= 50+50+10+110
N°25.- La selección peruana de voleibol está conformada por 12 chicas. ¿De cuántas formas se pueden conformar un equipo de 6 si se sabe que 2 chicas se niegan a jugar en el mismo equipo
Solución
El equipo de 6 chicas se puede presentar en los siguientes casos:
1er caso: Si no figura ninguna de las dos chicas que se niegan a jugar juntas, las seis chicas deben de escogerse de entre 10
C_{6}^10=\cfrac{10! }{(10-6)!6!}=210
2do caso: Si figura una de las dos chicas que se niegan a jugar juntas, las otras cinco chicas deben escogerse de entre las 10 restantes
C_{1}^2 x C_5^{10}=\cfrac{2! }{(2-1)!1!}x \cfrac{10! }{(10-5)!5!}=2 x 252=504
En total 210 + 504 = 714 formas
N°26.- ¿De cuántas maneras diferentes se pueden sentar 8 personas en una mesa redonda de 5 asientos, si 3 están en espera?
Solución
El número de grupos de 5 personas que se ubican en la mesa circular es:
C_{5}^8 =\cfrac{8! }{(8-5)!5!}=56
El número de formas en que cada grupo de 5 personas se pueden sentar en la mesa es:
P_{cir} =(5-1)=24
El total de formas es = 56 x 24 = 1344 maneras diferentes
CÁLCULO DE PROBABILIDADES DE EVENTOS COMPUESTOS
Los axiomas de la formulación moderna de la teoría de la probabilidad constituyen una base para deducir a partir de ellas un amplio número de resultados.
La letra P se utiliza para designar la probabilidad de un evento, siendo P(A) la probabilidad de ocurrencia de un evento A en un experimento.
AXIOMA 1: Si A es un evento de S, entonces la probabilidad del evento A es:
1 \le p (A) \le 1
Como no podemos obtener menos de cero éxitos ni más de n éxitos en n experimentos, la probabilidad de cualquier evento A, se representa mediante un valor que puede variar de 0 a 1.
AXIOMA 2: Si dos eventos son mutuamente excluyentes (o individuales), la probabilidad de obtener A o B es igual a la probabilidad de obtener A más la probabilidad de obtener B.
P(A \cup B ) =P(A)+P(B) Eventos Mutuamente Excluyentes
Excluirse mutuamente quiere decir que A y B no pueden ocurrir simultáneamente en el mismo experimento. Así, la probabilidad de obtener águila o sol en la misma tirada de una moneda será:
P(A \cup B ) =P(A)+P(B)
P(A \cup B ) =\cfrac{1}{2} + \cfrac{1}{2} =1
En general podemos decir que la suma de las probabilidades de todos los posibles eventos mutuamente excluyentes es igual a 1:
P(A_1)+P(A_2)+P(A_3)+...+P(A_n)=1
Suma De Eventos Mutuamente Excluyentes
AXIOMA 3: Si A es un evento cualquiera de un experimento aleatorio y A’ es el complemento de A, entonces
P(A´)=1P(A)
P(A)=P(A´)=1
P(A)=1-P(A´)
Es decir, la probabilidad de que el evento A no ocurra, es igual a 1 menos la probabilidad de que ocurra.
Probabilidades Subjetivas. Esto sucede cuando el único método disponible para asignar probabilidades es el juicio personal y la precisión de éstos depende de la habilidad individual para valorar correctamente una situación.
Eventos Mutuamente Excluyentes (o incompatibles). Son eventos definidos de manera que la ocurrencia de uno imposibilita la ocurrencia de los demás (si alguno de ellos sucede, los restantes no pueden suceder). Y que no tienen intersección entre ellos.
Diagramas de Venn
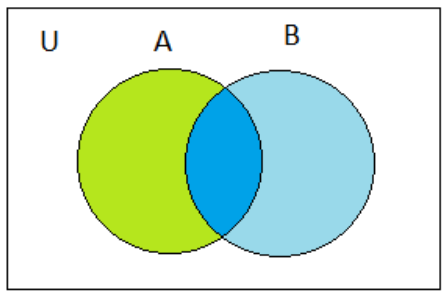

Eventos mutuamente excluyentes
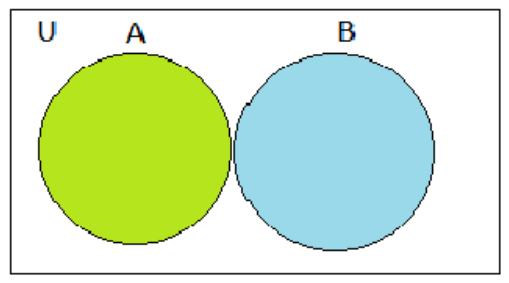

Eventos que no son mutuamente excluyentes
Nota. Decir P(A y B), es decir P(A ∩ B) y; decir P(A o B), es decir P(A ∪ B).
Regla de la Adición. Es la Probabilidad Compuesta P(A o B); en donde A y B son eventos mutuamente excluyentes (o incompatibles) y se aplica la siguiente regla. P(A o B) = P(A) + P(B). Pero, si los eventos A y B no son mutuamente excluyentes (o compatibles) se aplica la siguiente regla general:
P(A o B )=P(A)+P(B)-P(A \cap B)
Ejemplos.
1) Se lanzan dos dados y se definen tres eventos: A es la suma de los números en los dados igual a 7; B es la suma de los números en los dados igual a 10 y; C cada dado muestra el mismo número.
a) ¿Cómo son los eventos A y B; B y C y; A y C?
b) ¿Cuál es la probabilidad del evento A, B y C?
c) ¿Cuál es la probabilidad de A o B?
d) ¿Cuál es la probabilidad de B o C?
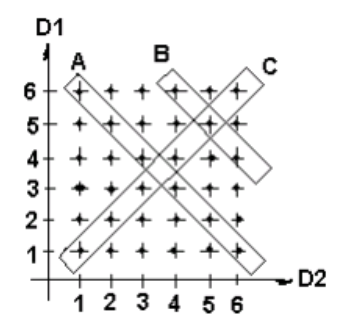

a) A y B son eventos mutuamente excluyentes (o incompatibles); B y C no son eventos mutuamente excluyentes (son compatibles) y; A y C son eventos mutuamente excluyentes (o incompatibles).
b) n(s)=36; n(A)=6; n(B)=3 y n(C)=6 P(A)=\cfrac{n(A)}{n(S)}=\cfrac{6}{36}=\cfrac{1}{6}=16.67\%
P(B)=\frac{n(B)}{n(S)}=\cfrac{3}{36}=\cfrac{1}{12}=8.3\% y P(C)=\cfrac{n(C)}{n(S)}=\cfrac{6}{36}=\cfrac{1}{6}=16.67%
c) P(A o B)=P(A)+P(B)=\cfrac{6}{36}+\cfrac{3}{36}+\cfrac{9}{36}=\cfrac{1}{4}=25%
d) P(B o C)=P(B)+P(C)-P(B \cap C)=\cfrac{3}{36}+\cfrac{6}{36}-\cfrac{1}{36}=\cfrac{8}{36}=\cfrac{2}{9}=22.22\%
2) En un grupo escolar, 80 mujeres y 60 hombres son estudiantes de tiempo completo y; 20 hombres y 40 mujeres son de tiempo parcial. Si se selecciona un alumno aleatoriamente, en la cual, el evento A es el alumno elegido de tiempo completo y, B el alumno seleccionado de tiempo parcial y además es hombre.
a) ¿Cuál es la probabilidad de los eventos A o B?
b) ¿cuál es la probabilidad de que el alumno sea mujer o de tiempo completo?
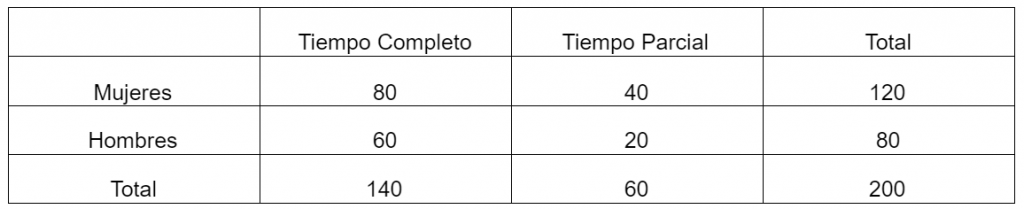

n(S)=200; n(A)=140; n(B)=20; n(M)=120; n(TC)=140; y n(M y TC)=80;
P(A)=\cfrac{n(A)}{n(S)}=\cfrac{140}{200}=\cfrac{7}{10}=70\%; P(B)=\cfrac{n(B)}{n(S)}=\cfrac{20}{200}=\cfrac{1}{10}=10\%;
P(M)=\cfrac{n(M)}{n(S)}=\cfrac{120}{200}=\cfrac{6}{10}=60\%; P(TC)=\cfrac{n(TC)}{n(S)}=\cfrac{140}{200}=\cfrac{7}{10}=70\%; y P(M y TC)=\cfrac{n(M y TC)}{n(S)}=\cfrac{80}{200}=\cfrac{4}{10}=40\%;
A Y B son eventos mutuamente excluyentes, por tanto
a) P(A o B) = P(A)+ P(B)=\cfrac{7}{10}+\cfrac{1}{10}=cfrac{8}{10}= 80\%
M y TC no son eventos mutuamente excluyentes, por tanto
b) P(M o TC) = P(M)+ P(TC) - P(M y TC)=\cfrac{7}{10}+\cfrac{6}{10}-cfrac{4}{10}=\cfrac{9}{10} 90\%
3) Una caja contiene 15 bolas de billar que están numeradas del 1 al 15. Se saca una bola al azar y el número se registra. Encuentre la probabilidad de que el número sea: a) par, b) Menor de 5, c) par y menor de 5, d) par o menor de 5
Solución:
a) Hay 7 números: 2, 4, 6, 8, 10, 12, 14, que son pares. Por lo tanto p=\cfrac{7}{15}
b) Hay 4 números: 1, 2, 3, 4, que son menores de 5. Por lo que p=\cfrac{4}{15}
c) Hay 2 números: 2 y 4, que son pares y menores de 5. De ahí que p=\cfrac{2}{15}
d) Por la regla de adición p=\cfrac{7}{15}+\cfrac{4}{15}-\cfrac{2}{15}=\cfrac{9}{15}
En forma alterna, hay 9 números: 1,2, 3, 4, 6, 8, 10, 12, 14 que son pares o menores de 5, de donde p=\cfrac{2}{15}
4) Si tiras una moneda y lanzas un dado ¿cuál es la probabilidad de que salga sol y un número par?
Primero hacemos una lista de cotejo con todos los resultados posibles. (Ca1 significa que la moneda caiga águila y que el dado caiga en un 1).


Hay 12 resultados posibles y tres de ellos nos dan los resultados deseados (sol más número par). Estos serían Cs2, Cs4 y Cs6:
P=\cfrac{3}{12}=\cfrac{1}{4}=25\%
5) Se tira un dado y se quiere determinar la probabilidad de que aparezca un número múltiplo de 3 o divisor de 10. Para que sea múltiplo de tres, tenemos los casos 3 y 6. Para que sea un divisor de 10, tenemos los casos 1, 2 y 5. Se observa que es imposible que se cumplan ambos eventos, ya que no hay ningún elemento común. En este caso se dice que son eventos excluyentes o incompatibles. Por lo tanto, la probabilidad de que aparezca un número múltiplo de tres o divisor de 10 es:
(A) = múltiplo de 3; P (B) = divisor de 10;
P(A o B)=P(A)+P(B)=\cfrac{2}{6}+\cfrac{3}{6}=\cfrac{5}{6}
6) Extraer una carta de un mazo inglés de 52 cartas y queremos determinar la probabilidad de sacar un as o un trébol. Para que sea un as hay cuatro posibilidades. Para sacar un trébol hay trece posibilidades. Pero en este caso, hay un elemento que es común a ambos eventos (el as de trébol), y por lo tanto los casos favorables serían 4 + 13 – 1 = 16; en términos de probabilidades sería equivalente a afirmar que A y B son eventos compatibles, es decir, si pueden ocurrir ambos simultáneamente, la probabilidad se calcula mediante la expresión:
P(A o B)=P(A)+P(B)-P(A y B)
P(As)+P(\text{Trébol})-P(\text{As y Trébol)})= \cfrac{4}{52}+ \cfrac{13}{52}-\cfrac{1}{52}=\cfrac{16}{52}=\cfrac{4}{13}
7) Una caja contiene 4 canicas rojas, 3 canicas verdes y 2 canicas azules. Una canica es eliminada de la caja y luego reemplazada. Otra canica se saca de la caja. ¿Cuál es la probabilidad de que la primera canica sea azul y la segunda canica sea verde?
Ya que la primera canica es reemplazada, el tamaño del espacio muestral (9) no cambia de la primera sacada a la segunda así los eventos son independientes.
P (azul luego verde) = P (azul) · P (verde)
\cfrac{2}{9} \cdot \cfrac{3}{9}=\cfrac{6}{81}=\cfrac{2}{27}
8.- Se tienen cinco libros de distintas materias: Matemática, Biología, Química, Física y Lenguaje. Si se toma uno de ellos, ¿cuál es la probabilidad de que este sea de matemática o de física?
Solución:
Sean los eventos
A =Tomar el libro de Matemáticas.
B = Tomar el libro de Física.
La probabilidad pedida es: P(A∪B) = P(A) + P(B) -P(A∩B) Como A y B son eventos mutuamente excluyentes, P(A∩B) = 0. Por lo tanto, la probabilidad pedida nos queda:
P(A \cup B)=\cfrac{1}{5}+\cfrac{1}{5} - 0 =\cfrac{2}{5}
9.- Se elige al azar un número entero positivo del 1 al 19. ¿Cuál es la probabilidad de que el número sea múltiplo de 3 ó de 5?
Solución:
Como son 19 números, la cantidad de elementos del espacio muestral es #E = 19. Sean los eventos: A = Obtener un número múltiplos de 3, B = Obtener un número múltiplos de 5. Si podemos identificar la cantidad de elementos del espacio muestral A∪B lo resolvemos directamente como sigue:
(A \cup B)=\{ 3,5,6,9,10,12,15,18\} \Rightarrow \# A\cup B =8 \Rightarrow P(A\cup B)= \cfrac {\#(A \cup B)}{\# E}= \cfrac{8}{19}
EVENTOS INDEPENDIENTES
Se dice que dos eventos son independientes cuando la ocurrencia de uno no afecta la ocurrencia del otro. Si tiramos una moneda tres veces, la probabilidad de que en todas las ocasiones salga cara responde a eventos independientes, ya que el resultado de un lanzamiento no afecta lo que vaya a ocurrir en el próximo.
Si configuramos un diagrama de árbol para el conteo de todas las posibilidades en el lanzamiento de tres monedas, obtenemos el siguiente gráfico:
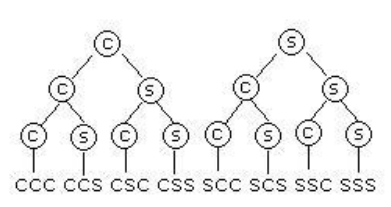

Según este diagrama, la probabilidad de obtener tres resultados cara es \cfrac{1}{8} lo que es equivalente a multiplicar la probabilidad de obtener cara en cada lanzamiento:
P(cara, cara y cara)= \cfrac{1}{2} \cdot \cfrac{1}{2} \cdot \cfrac{1}{2} = \cfrac{1}{8}
En general, si A y B son eventos independientes, entonces se cumple que: P(\text{A y B} )= P(A) \cdot P(B)
1.- Ejemplo:
Se ha encontrado que en la ciudad de México, la distribución de los cuatro grupos sanguíneos básicos es como sigue: O es el 45%; A el 40%; B el 10%; AB el 5%. ¿Cuál es la probabilidad de que en una pareja de cónyuges de la ciudad de México, seleccionada al azar?:
a) Ambos sean tipo A
b) Ninguno sea tipo O
c) La esposa sea tipo A y el esposo tipo B
d) Uno sea tipo A y el otro tipo B
e) Los dos sean tipos diferentes
Solución:
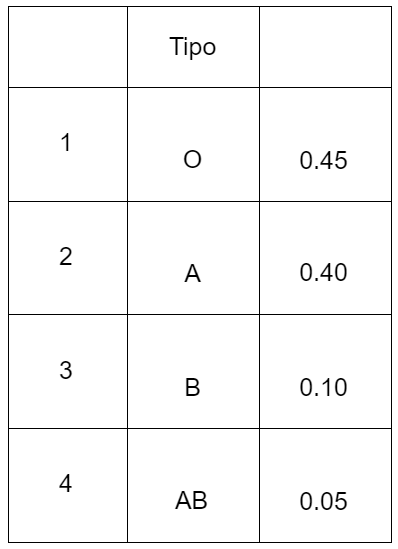

a) P(\text{A y A})=(0.40)(0.40)= 0.16
b) P(\text{0´ y 0'})=(0.55)(0.55)= 0.30
c) P(\text{A y B})=(0.40)(0.10)= 0.04
d) P(\text{A y B})=(0.40)(0.10)2= 0.08
e) \hspace{0.5cm}P(\text{O y A})= (0.45)(0.40)2= 0.36
\hspace{0.5cm}P(\text{O y B})= (0.45)(0.10)2= 0.09
\hspace{0.5cm}P(\text{O y AB})= (0.45)(0.05)2= 0.045
\hspace{0.5cm}P(\text{A y B})= (0.40)(0.10)2= 0.08
\hspace{0.5cm}P(\text{A y AB})= (0.40)(0.05)2= 0.04
\hspace{0.5cm}P(\text{B y AB})= (0.10)(0.05)2= 0.01
= \hspace{1cm} 0.625
2.-Ejemplo
Tres automóviles A, B y C compiten en tres carreras separadas, y las probabilidades de que cada uno gane su carrera son \frac{1}{2}, \frac{1}{3} \text{ y } \frac{1}{4} , respectivamente. Calcule la probabilidad de que:
a) Ninguno gane su carrera
b) Solamente uno gane su carrera
c) Solamente dos ganen sus carreras
d) Los tres ganen sus carreras
Solución:
a)\text{ P(Ninguno)}= \left ( \frac{1}{2} \right ) \left ( \frac{2}{3} \right ) \left ( \frac{3}{4} \right )=\frac{1}{4}
b)\text{ P(1 gane )}=\left ( \frac{1}{2} \right ) \left ( \frac{2}{3} \right ) \left ( \frac{3}{4} \right )=\frac{1}{4}
\left ( \frac{1}{2} \right ) \left ( \frac{1}{3} \right ) \left ( \frac{3}{4} \right )=\frac{1}{8}
\left ( \frac{1}{2} \right ) \left ( \frac{2}{3} \right ) \left ( \frac{1}{4} \right )=\frac{1}{12}
\hspace{1cm} = \frac{11}{24}
c)\text{ P(solo 2 ganen )}= P(A,B)=\left ( \frac{1}{2} \right ) \left ( \frac{1}{3} \right ) \left ( \frac{3}{4} \right )=\frac{3}{24}
= P(A,C)=\left ( \frac{1}{2} \right ) \left ( \frac{1}{4} \right ) \left ( \frac{2}{3} \right )=\frac{2}{24}
= P(B,C)=\left ( \frac{1}{3} \right ) \left ( \frac{1}{4} \right ) \left ( \frac{1}{2} \right )=\frac{1}{24}
\hspace{1.5cm} =\frac{1}{4}
d)\hspace{0.5cm}\text{ P(3 ganen )}= \left ( \frac{1}{2} \right ) \left ( \frac{1}{3} \right ) \left ( \frac{1}{4} \right )=\frac{1}{24}
3.-Ejemplo:
La probabilidad de que un hombre viva 20 años más es \frac{1}{4} y que su mujer viva 20 años más es \frac{1}{3}. Calcular la probabilidad:
a) De que ambos vivan 20 años
b) De que el hombre viva 20 años y su mujer no
c) De que ambos mueran antes de los 20 años.
Solución:
a) Como \text{A y B} son eventos independientes
P(\text{A y B})= P(A)\cdot P(B)= \frac{1}{4} (\frac{1}{3})=\frac{1}{12}
b) Como P(B)= \frac{1}{3} el complemento será P(B´)= \frac{2}{3} y son eventos independientes
P(\text{A y B})= P(A)\cdot P(B)= ( \frac{1}{4}) \frac{2}{3}=\frac{1}{6}
c) P(A´)= \frac{3}{4} Por ser eventos independientes
P(\text{A´ y B´})= P(A´)\cdot P(B´)= ( \frac{3}{4}) \frac{2}{3}=\frac{1}{2}
4.-Ejemplo
En una urna hay 2 bolas rojas, 2 azules y 2 verdes. Se extraen 2 bolas con reemplazamiento:
a) ¿Cuál es la probabilidad de que sean del mismo color?
b) ¿Cuál es la probabilidad de que sean de distinto color?
Realizamos el diagrama de árbol, teniendo en cuenta que para la segunda extracción tenemos las mismas probabilidades que en la primera extracción, ya que tenemos las mismas bolas en la urna:
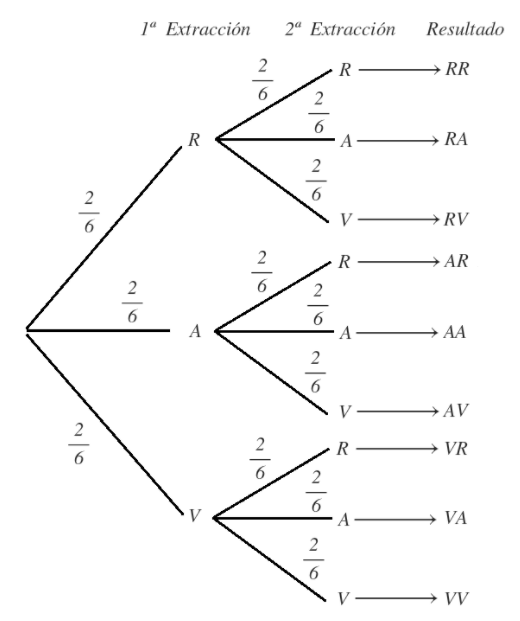

Las probabilidades de cada resultado son:
P(RR)= \cfrac{2}{6} \cdot \cfrac{2}{6}=\cfrac{4}{36}=\cfrac{1}{9}
P(RA)= \cfrac{2}{6} \cdot \cfrac{2}{6}=\cfrac{4}{36}=\cfrac{1}{9}
P(RV)= \cfrac{2}{6} \cdot \cfrac{2}{6}=\cfrac{4}{36}=\cfrac{1}{9}
P(AR)= \cfrac{2}{6} \cdot \cfrac{2}{6}=\cfrac{4}{36}=\cfrac{1}{9}
P(AA)= \cfrac{2}{6} \cdot \cfrac{2}{6}=\cfrac{4}{36}=\cfrac{1}{9}
P(AV)= \cfrac{2}{6} \cdot \cfrac{2}{6}=\cfrac{4}{36}=\cfrac{1}{9}
P(VR)= \cfrac{2}{6} \cdot \cfrac{2}{6}=\cfrac{4}{36}=\cfrac{1}{9}
P(VA)= \cfrac{2}{6} \cdot \cfrac{2}{6}=\cfrac{4}{36}=\cfrac{1}{9}
P(VV)= \cfrac{2}{6} \cdot \cfrac{2}{6}=\cfrac{4}{36}=\cfrac{1}{9}
La probabilidad de que las dos bolas sean del mismo color es:
P(\text{mismo color })= P(RR)+P(AA)+P(VV)=
=\cfrac{1}{9} + \cfrac{1}{9} +\cfrac{1}{9}=\cfrac{3}{9}=\cfrac{1}{3}
La probabilidad de que las dos bolas sean de distinto color es:
=P(RA)+P(RV)+P(AR)+P(AV)+P(VR)+P(VA)=
=\cfrac{1}{9}+\cfrac{1}{9}+\cfrac{1}{9}+\cfrac{1}{9}+\cfrac{1}{9}+\cfrac{1}{9}=\cfrac{6}{9}=\cfrac{2}{3}
5.-Ejemplo
De dos tiradores se sabe que uno de ellos hace dos aciertos de cada tres disparos, y el otro consigue tres aciertos de cada cuatro disparos. Si los dos disparan simultáneamente, halle la probabilidad de que:
a) Ambos acierten. b) Uno acierte y el otro no.
c) Ninguno de los dos acierte. d) Alguno acierte
Definimos los suceso siguientes :
T_1 = \{ \text{el primer tirador acierta } \}
T_2 = \{ \text{el segundo tirador acierta } \}
Aplicamos la probabilidad de la intersección de sucesos independientes
P(A_1 \cap A_2 \cap ...\cap A_n)=P(A_1) \cdot P(A_2) \cdot ...\cdot P(A_n)
a)
P(\text{ambos tiradores acierten} )=P(T_1 \cap T_2)= \cfrac{2}{3} \cdot \cfrac{3}{4}=\cfrac{6}{12}= \cfrac{1}{2}
b)
P(\text{uno acierte y el otro no} )=P(T_1 \cap \bar{T_2})+ P(\bar{T_1} \cap T_2)= \cfrac{2}{3} \cdot \cfrac{1}{4}+\cfrac{1}{3} \cdot \cfrac{3}{4}=\cfrac{2}{12}+\cfrac{3}{12}=\cfrac{5}{12}
c)
P(\text{ninguno de los dos acierte} )=P(\bar{T_1} \cap \bar{T_2})= \cfrac{1}{3} \cdot \cfrac{1}{4}=\cfrac{1}{12}
d)
P(\text{alguno acierte} )=P(T_1 \cup T_2)= 1-P (\bar{T_1} \cap \bar{T_2})=1 - \cfrac{1}{12}=\cfrac{11}{12}
6.-Ejemplo
La probabilidad de que un vuelo se retrase es 0,2 (= 20%), ¿cuáles son las probabilidades de que no haya demoras en un viaje de ida y vuelta?
La probabilidad de que un vuelo no tenga un retraso es 1 − 0,2 = 0,8, por lo que estos son todos los resultados posibles:
0.8 × 0.8 = 0.64 probabilidad de no retras
0.2 x 0.8 = 0.16 probabilidad de demora en el 1er vuelo
0.8 x 0.2 = 0.04 probabilidad en ambos vuelos
0.2 x 0.2 = 0.04 probabilidad de demora en ambos vuelos
Cuando sumamos todas las probabilidades obtenemos
0.64 + 0.16 +0.16 +0.4 =1.0
Todos se suman y dan 1,0, que es una buena manera de verificar nuestros cálculos.
Resultado: 0.64, o una probabilidad de 64% de no demoras
7.-Ejemplo
Imagina que hay dos grupos:
- Un miembro de cada grupo es elegido al azar para el círculo de ganadores,
- después uno de esos es elegido al azar para obtener un gran premio de dinero:
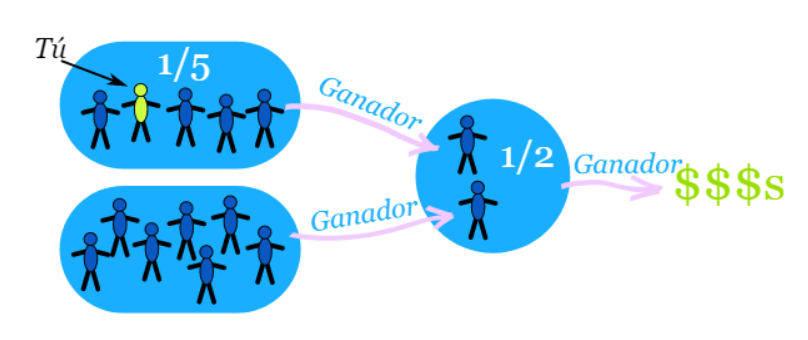

¿Cuál es su probabilidad de ganar el gran premio?
hay una probabilidad de 1/5 de ir al círculo de ganadores
y 1/2 de probabilidad de ganar el gran premio
Entonces tienes una probabilidad de 1/5 seguida de una probabilidad de 1/2 … lo que hace una probabilidad de 1/10 en general:
También podemos calcular usando decimales (1/5 es 0.2 y 1/2 es 0.5):
0.2 x 0.5 = 0.1
Entonces, tu probabilidad de ganar el premio grande de dinero es 0.1 (que es lo mismo que 1/10).
8.- Ejemplo
En una empresa trabajan hombres y mujeres, además se sabe que un 15% de los empleados se han perfeccionado en el extranjero. Si el 35% son mujeres, ¿cuál es la probabilidad de que al escoger una persona de la empresa, esta sea mujer y se haya perfeccionado en el extranjero?
P(mujer) = 35/100
P(perfeccionado extranjero) = 15/100 Como son eventos independientes
P(M ∩ E) = 35/100 15/100 = 21/400 = 5.25%
9.-Ejemplo
De una baraja estándar de 52 cartas sea A el suceso de sacar un As en la primera extracción y B sacar un Rey en la segunda extracción. Calcular la probabilidad de sacar un As y un Rey en dos extracciones devolviendo la carta extraída.
Solución:
A y B son sucesos independientes porque la ocurrencia de A no afecta la probabilidad de ocurrencia de B.
La probabilidad de que la primera carta sea un As es: P(A) \cfrac{4}{52} , P (B/A)= P(B)=\cfrac{4}{52}
Reemplazando los anteriores valores en la regla particular de la multiplicación se obtiene:
P(\text {A y B }) = P(A) \cdot P(B)=\cfrac{4}{52} \cdot \cfrac{4}{52}=\cfrac{16}{2704}=\cfrac{1}{169}
