Índice del Contenido
Carl Friedrich Gauss
Nacido en Brunswick Alemania en el año de 1777, de origen humilde, popularmente conocido en el mundo simplemente como Gauss, tuvo suerte de poder desarrollar su talento matemático en una época donde las matemáticas eran practicadas como pasatiempo por aficionados y personas privilegiadas de la alta sociedad, su padre se oponía a que fuera a la escuela ya que consideraba que no era de importancia para su hijo.
Durante su vida, desarrolló trabajos en las mas diversas áreas de la ciencia como la geometría, álgebra, estadística, física, astronomía, análisis numérico etc. los cuales por fortuna para la humanidad fueron resguardados, quedando registrados en cartas y publicaciones. Sin embargo, Gauss era muy cuidadoso de su trabajo, protegía sus notas utilizando un lenguaje cifrado quedando algunos códigos en sus notas que nunca descifró y no se sabe actualmente a que se refería.
Además de cuidadoso fue muy exigente consigo mismo, condicionándose a no publicar resultados parciales, esperaba hasta terminar por completo su trabajo matemático para difundirlo, ya que decía que un buen trabajo es aquel al que no se le puede agregar, quitar o modificar nada que cambie su esencia. Esta forma de divulgar su trabajo, generó numerosas controversias por la autoría de sus teorías y descubrimientos, controversias que fueron resueltas muchos años después al estudiar su diario.

Esta forma de publicar, le ganó algunas rencillas con matemáticos de su época, como el Matemático Adrien-Marie Legendre uno de sus mas grandes rivales con el cual compitió por mucho tiempo en diversas áreas de la ciencia. Se dice que si Gauss hubiera publicado sus trabajos mientras los desarrollaba, las matemáticas hubiesen avanzado mas rápido ahorrando a la humanidad mucho tiempo, ya que posteriormente muchos matemáticos tardaron años en lograr demostrar sus resultados por que Gauss no dejo registro del método que siguió para llegar a ellos, uno de sus lemas era:
“Las matemáticas son como una obra arquitectónica;
Un arquitecto jamás dejaría los andamios para que la
gente viera como se había construido el edificio “
A Gauss debemos mucho sobre como se abordan los problemas en las matemáticas actuales, la estructura lógica que se sigue para los planteamientos matemáticos, enunciando resultados o teoremas acompañados de su demostración para finalizar con corolarios o consecuencias, es la forma mas aceptada de presentar conclusiones o resultados actualmente, y una vez más la exigencia que tenia hacia su trabajo le impedía presentar resultados no demostrados, esto pudiese ser obvio en nuestros días, pero previo a la época de Gauss, el rigor con el que se demostraban las matemáticas solo era superficial y especulativo, es decir no le daban tanta importancia al por que funcionaban las matemáticas.
“Las matemáticas son la reina de
las ciencias y la aritmética es la reina de las matemáticas “
Una de sus primeros trabajos a la temprana edad de 19 años fue la construcción del heptadecágono, un problema o mejor dicho un reto matemático planteado desde los orígenes de la geometría griega. Este reto consiste en la construcción de un polígono regular de 17 lados utilizando sólo regla y compás, además de algunas otras consideraciones para hacer el reto aún más complejo, este hecho fue de tal importancia para él, que a partir de la solución de este, decidió dedicarse por completo a construirse una carrera en el terreno de la ciencia y las matemáticas.
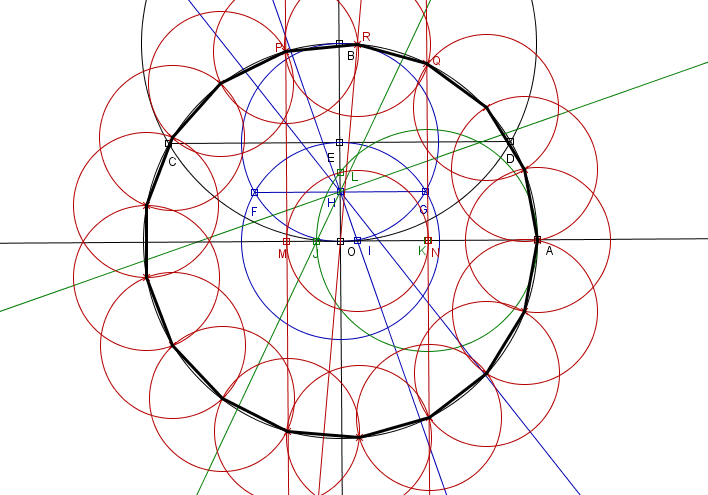
Este logro perduro tanto en su mente que incluso pidió que en su tumba se esculpiera un heptadecágono, curiosamente no fue posible ya que este polígono, como se puede apreciar casi no se distingue de un circulo, así que el encargado de su tumba decidió que en vez de esculpir un heptadecágono, grabaría una estrella de 17 picos, incluso en la actualidad continua sin tener dicha figura en su lapida.
Como se puede observar en el vídeo la construcción es compleja, ya que esta compuesta de numerosos pasos intermedios con trazos muy pequeños, incluso en el vídeo se puede apreciar que hace trazos a ojo para ahorrar tiempo y finalmente llega a una burda aproximación, el cual forza con el último trazo para obtener los 17 lados, quedando un polígono no muy regular.
Sin embargo con esto podemos darnos una idea de la complejidad del problema y la genialidad de Gauss para resolverlo sin la necesidad de hacer medidas.
Te Puede Interesar:
FRACTALES
” LA GEOMETRÍA DE LA NATURALEZA “
¿Es posible construir cualquier polígono con el uso de regla y compás?
Una vez resuelto dicho problema Gauss, fue mas allá, haciéndose esta pregunta, algo muy natural dentro de su mente curiosa y a lo largo de su labor encontró que este problema esta relacionado, con la forma de dividir una circunferencia, con lo cual publicaría numerosos resultados sobre circunferencias llegando a la conclusión en 1801, que un polígono regular de n lados puede ser construido exclusivamente con regla y compás, solo si cumplen con la característica, que el numero de lados cumplan ciertas condiciones dentro de los llamados números de Fermat.
Inicio de sus Estudios Profesionales.
Una de sus primeras aportaciones a las matemáticas ya como profesional, a los 22 años, fue en 1799 en su tesis de licenciatura en la Universidad de Helmstedt, la cual llevaba como titulo Nueva demostración del teorema que dice “Toda función algebraica racional puede descomponerse en factores de primer o segundo grado con coeficientes reales ”, la cual resulto en la primera demostración del Teorema fundamental del álgebra.
Durante el desarrollo de su tesis fue encontrando caminos que le fueron llevando a nuevos descubrimientos y nuevos planteamientos por ejemplo durante la demostración del Teorema fundamental del álgebra donde a grandes rasgos se buscan las raíces de polinomios elevados a exponentes cada vez mas grandes, un problema que ha sido un clásico para los estudiosos de esta materia, llevo a Gauss a incorporar conjuntos de números para dar solución a dichos polinomios ampliando cada vez mas los recursos numéricos para lograr una resolución, iniciando con los números naturales llegando hasta los números complejos a los cuales doto de una representación geométrica y una aritmética para poder hacer todo tipo de operaciones con ellos. Algo controvertido para la época donde las representaciones gráficas no eran vistas con buenos ojos entre los matemáticos por ser consideradas poco fiables.
Para comprender la relevancia de la Tesis de Gauss su teorema fue considerado como el trabajo que daba la pauta para resolver polinomios de grado n cualquiera, generando tal revuelo entre sus colegas, que lo puso en ese momento dentro de los matemáticos mas grandes de la historia aludiendo a personajes consolidados como Euler, Lagrange y Laplace.
El libro de los Siete Sellos
Uno de sus primeros libros llamado “Disquisitiones Arithmeticae” también conocido como” El libro de los Siete Sellos” un trabajo que da origen a la teoría de números, actual rama de las matemáticas que se enfoca en el estudio de las propiedades de los números, siendo considerada como una obra fundamental para esta nueva disciplina.
Sin embargo a pesar de tan novedoso planteamiento, no fue bien recibida por la Academia Matemática de París, autoridad académica que validaba la mayoría de aportaciones, considerándola una obra extremadamente compleja por su lenguaje, aunado a que Gauss no facilitaba su comprensión, ocultando la mayor parte de los “andamios” sobre los que construyó su obra, llego a ser clasificada como oscura y densa, ganándose de ahí el sobrenombre de ” El libro de los Siete Sellos” . Ya que su lectura es complicada incluso para los expertos en el tema.
Por fortuna surgieron matemáticos que dedicaron gran parte de su trabajo a debelar los secretos dentro de esta obra, como el matemático alemán Johann Peter Gustav Lejeune Dirichlet quien fue uno de los primeros en quebrar los siete sellos, se dice que siempre tenia a la mano una copia de Disquisitiones Arithmeticae en su escritorio incluso cerca de su cama.

¿Cuáles eran los Secretos Guardados en Disquisitiones Arithmeticae ?
Para empezar el libro esta compuesto por 7 capítulos, los primeros tres ( I, II, III ) son la introducción para poder entrar a los capítulos IV, V, VI, siendo estos la parte cumbre de esta obra y finalmente el capitulo VII dedicado a su primer descubrimiento.
Capitulo I Inicia hablando sobre los conceptos básicos las reglas de la divisibilidad para 3, 9 y 11 y define el criterio de congruencia.
Capitulo II Desarrolla el concepto de congruencia ya que es algo fundamental para su planteamiento, y continua desarrollando dicho concepto hasta sentar las bases de lo que llegará a ser el álgebra modular algo fundamental en nuestros días.
Capitulo III Llamado “El resto de las Potencias” se habla sobre los residuos cuadráticos y de potencias superiores, inicia demostrando el pequeño Teorema de Fermat, utilizando como herramienta la formula del binomio cuadrado de Newton, adaptada a congruencias. Una vez planteados los capítulos anteriores los cuales sirven de preparación para lo que el consideraba su mayor aportación el Capitulo IV.
Capitulo IV Gauss llega a uno de sus resultados centrales, la conocida “Ley de reciprocidad cuadrática”, la cual fue enunciada primeramente por Leonhard Euler en 1742, a la cual el matemático Adrien-Marie Legendre en 1798 también intento demostrar con poco éxito, quedando finalmente demostrada de forma contundente por Gauss.
Capitulo V Trabaja con las expresiones llamadas por Euler “Formas Cuadráticas” donde inicia unificando los trabajos previos realizados por el matemático Lagrange sobre estas formas, para enfocarse en la clasificación de las formas cuadráticas y sus propiedades a partir de sus discriminantes, finalizando con una demostración de los números triangulares.
Capitulo VI En este capitulo presenta aplicaciones de los resultados encontrados en las secciones anteriores, principalmente habla sobre fracciones parciales, el como descomponer una fracción, la cual es empleada para la integración de funciones racionales, describe a los números decimales periódicos y la solución de congruencias, establece criterios para distinguir números primos sin la necesidad de hacer cálculos engorrosos.
Capitulo VII Finalmente el y sin duda uno de los mas populares dentro de la divulgación de su trabajo, el cual amplía uno de sus resultados hallado durante su juventud “La división del circulo con regla y compás “ donde incluyó su famoso polígono de diecisiete lados, además de todas sus investigaciones relacionadas con la construcción de polígonos regulares.
Además de los increíbles resultados que cada Capitulo de su libro dieron al mundo, podemos agregar que la culminación y publicación de este, su gran libro se dieron antes de que Gauss cumpliera lo 30 años de edad.
Primer Éxito en el Campo de la Astronomía
Desde la época de Nicolás Copérnico se había considerado que la distancia entre el planeta Marte y Júpiter era misteriosamente grande, lo cual llevo a los astrónomos de aquel tiempo a buscar una ley que explicara dicha extrañeza y con esta, poder descubrir nuevos planetas.
Todo inicio el 1 de Enero de 1801 en el observatorio de Palermo cuando el astrónomo Giuseppe Piazzi descubrió lo que para ese momento era la definición de un planeta (lo que en la actualidad se conoce como un planeta enano), al cual llamó Ceres Ferdinandea, Ceres en honor a la diosa Romana de la agricultura, patrona de Sicilia y Ferdinandea por el Rey Fernando IV de Nápoles y Sicilia.

Este descubrimiento desató un gran entusiasmo entre la comunidad científica, el comportamiento a primera vista de este nuevo planeta aparentó ser regido por las leyes astronómicas propuestas por Titus-Bode en 1768, las cuales servían de guía para la exploración sistemática del sistema solar, con lo cual se genero gran confianza en la comunidad científica asumiendo que ahora eran capaces de interpretar la naturaleza a profundidad, a tal grado que se pueden hacer predicciones extremadamente certeras, ya que hasta ese momento se creía que la humanidad estaba sometida a los caprichos inestructurados de la naturaleza, haciendo que los avances del siglo XVIII, el hombre se posicionara como el dueño de su destino.

Sin embargo lo que rápidamente se coloco como una gran victoria del conocimiento humano, se convirtió con la misma rapidez en una gran decepción pocas semanas después, cuando el nuevo cuerpo celeste desapareció y reapareció la noche del 11 de Febrero, este hecho represento una gran prueba, a lo cual la comunidad científica se mostró incapaz de determinar a donde volvería a aparecer. Cabe mencionar que durante la visibilidad de Ceres, Giuseppe Piazzi tomo datos de observación mediante su telescopio, sin embargo durante sus observaciones callo enfermo de gripa y cuando se reincorporo para continuar el seguimiento del astro, este había desaparecido.
Con lo cual el corto periodo de observaciones no le permitió construir la órbita que describía el movimiento de Ceres, con la que podriría predecir donde volvería a aparecer. Los datos recabados solo trazaban un arco de unos pocos grados de la órbita, con estos escasos datos se convocó a los astrónomos mas renombrados del momento para calcular dicha órbita, pero no tuvieron éxito.
Uno de los lideres de este grupo el renombrado astrónomo Franz Xaver von Zach decidió enviar los datos a un joven matemático de 24 años cuya fama estaba expandiéndose por toda Alemania, este matemático de nombre Gauss, realizo cálculos con los datos que le fueron envidados, y regreso en respuesta una estimación de la órbita, la cual distaba mucho de las suposiciones calculadas por el grupo de astrónomos, Pero al no contar con mas alternativas el astrónomo Franz von Zach decidió darle una oportunidad a las predicciones de Gauss con las que la noche del 7 de Diciembre lograron situar de nuevo al planeta siendo confirmado posteriormente el 1 de Enero de 1802 por miembros del grupo de trabajo liderado por Von Zach los cuales afirmaron con toda certeza que el planeta observado cumplía con las características del cuerpo celeste observado por Piazzi un año a tras, describiendo la órbita calculada por Gauss.
En Marzo de 1802 el astrónomo y médico Heinrich Olbers descubrió otro objeto llamado “Palas” de tamaño menor que Ceres y haciendo uso de la genialidad de Gauss calculó su órbita siendo testigo de las técnicas matemáticas de este y no quedándole duda que dicha solución no cabía en la casualidad, estaba ante uno de los mayores genios de la época.
Este echo detono la popularidad de Gauss en la comunidad científica internacional y gracias a esta predicción además de reconocerle el ser uno de los matemáticos mas notables, lo volvió el astrónomo mas popular de toda Europa. Concediéndole diversos reconocimientos como el nombramiento de la Real Sociedad de Ciencias de Gotinga, también tuvo invitaciones para dirigir el centro astronómico de San Petersburgo Rusia y el nuevo Observatorio de Gotinga que todavía se encontraba en construcción, por el cual se decidió finalmente.
Lo interesante de este acontecimiento fue que al resolver el planteamiento realizado por Franz von Zach en relación con el cálculo de la órbita de Ceres, Gauss había desarrollado una de las herramientas matemáticas mas potentes en la historia practica de las matemáticas, el llamado Método de mínimos cuadrados. El cual trabaja bajo la teoría de un método iterativo en el cual se van encontrando soluciones parciales, las que sirven de base para encontrar nuevos resultados mas cercanos a la solución real del problema. Esta técnica de optimización matemática tiene como objetivo dar con la función que mejor se adapte a los datos, además de ir calculando los errores o desviaciones y que su sumatoria sea la menor posible.
Gauss publicó sus aportaciones sobre el método de mínimos cuadrados hasta 1809 en su trabajo llamado “EL movimiento de las secciones Cónicas de los Cuerpos Celestes del sistema Solar “ casi una década después de haberlo utilizado en el cálculo de la órbita de Ceres, lo que le llevó a una disputa una vez más con el matemático Legendre, quien fuera el primero en publicarlo, en su trabajo “Nuevos métodos para la determinación de órbitas de cometas” en 1805 cuatro años antes que Gauss, siendo Legendre el que bautizará con el nombre que conocemos actualmente a este Método.
Sin embargo el trabajo realizado por Gauss y Heinrich Olbers calculando la orbita de Palas le dio la razón una vez más a Gauss, habiéndolo utilizado mucho antes de ser publicado por Legendre.
En el vídeo anterior se puede tener una idea mas clara a partir del minuto 4 de como trabaja el Método de los mínimo cuadrados en el cálculo de funciones a partir de pares de coordenadas.
Domando a los Números más Rebeldes
“ Los Números Primos “
La prueba mas antigua sobre el interés de la humanidad en estos números data del año 6500 a.C. la cual es un hueso que fue encontrado en el norte de África en 1960, tiene una serie de marcas estructuradas en columnas registrado los números 11, 13 , 17 y 19 que son los números primos comprendidos en el rango del 10 al 20 , también se pueden encontrar registros en la antigua china donde curiosamente se les dotaban de cualidades viriles por no ser posible su descomposición en números menores.
La cultura griega los estudió con gran interés llegando a identificar, la primera propiedad importante de estos la cual enunciaba: ” Todo numero natural puede descomponerse de forma única como el producto de números primos “ , estableciendo a los números primos como los constructores sobre los que se cimentaba toda la aritmética de los números, es como si fueran los elementos de los que esta constituido el universo matemático.
Uno de los personajes más antiguos de los que se tiene registro que dedicó gran parte de su vida al estudio, pero sobre todo al registro de estos fue Eratóstenes en la antigua Alejandría quien escribió tablas de números primos en el siglo III a.C. Además de crear un método relativamente sencillo para saber que numeros son primos dentro de un rango dado, a este método se le conoce como “La Criba de Eratóstenes “.
¿Los números primos son Infinitos ?
Posteriormente Euclides también se intereso por los números primos y se auto formulo varias preguntas, una de ellas era si estos números son infinitos, pregunta a la cual respondió utilizando el poder de razonamiento matemático puro, haciendo una demostración denominada por reducción al absurdo y evitando calcular números primos obsesivamente, desde la cual concluyó que efectivamente “La cantidad de números primos es mayor que cualquier número que se pueda pensar “, por lo tanto quedó descartada la idea de construir una tabla que contuviera todos estos enigmáticos números.

Estos números pasaron por varios matemáticos quienes hicieron diversos planteamientos como Pierre de Fermat el cual creyó haber encontrado una formula para generar números primos bajo ciertas condiciones muy específicas a dichos resultados se les coció como “Primos de Fermat” hasta ser refutada por Euler quien encontró que el quinto numero de Fermat algo casi imposible de calcular en aquella época, no era primo ya que era divisible entre 641 por lo cual los matemáticos prefieren llamarlos solo ” Números de Fermat “,
Este tema apasiono a Gauss durante toda su vida, sin duda uno de los retos matemáticos mas increíbles en la historia de las matemáticas y la ciencia en general. La aportación de Gauss a este tema fue un enfoque totalmente diferente, aplicando un pensamiento divergente, abordó el problema desde otra perspectiva, en vez de buscar todos los números primos o una expresión matemática que los genere, se decidió por analizar la distribución de estos, es decir si existía algún orden de distribución en intervalos determinados y utilizo como herramienta los logaritmos neperianos para buscar la relación posible de estos con su aparición.
Al iniciar sus investigaciones llego a una primera conclusión, los números primos no están distribuidos de manera uniforme, al ir avanzando y analizando la distancia media entre números primos consecutivos la cual aumenta a medida que aumenta el limite superior del rango analizado, la distancia media empieza a tener un comportamiento muy peculiar, lo cual resulta que para valores superiores a 10,000 el incremento de la distancia media se mantiene en 2.3 , este comportamiento generó que Gauss se formulara una hipótesis, donde incluía este hallazgo para estimar el orden de aparición de los números primos.
Gauss registro esta aproximación en su libro de logaritmos pero al no tener una demostración que la respaldara los archivó por un largo tiempo. En 1798 el matemático Legendre dio a conocer resultados de una de sus investigaciones relacionadas entre logaritmos y números primos, una vez más regreso la disputa por investigaciones orientadas hacia el mismo campo, y en 1808 Legendre publico el libro “Teoría de Números “ con su hipótesis pese a no tener el sustento de una demostración.
La respuesta de Gauss fue mejorar su propuesta matemática y concluyó planteándola como un cálculo de probabilidades la que es conocida como “Teorema de los Números Primos de Gauss” con el tiempo se comprobó que el planteamiento de Gauss era mas preciso que el de Legendre.
Te Puede Interesar:
NÚMEROS PRIMOS
” LOS NÚMEROS REBELDES “
De la Geometría a la Teoría de la Relatividad.
En 1818 el reino de Hannover le encargó a Gauss la triangulación y medición del Estado, tema relacionado con la Geodesia con lo cual se buscaba encontrar las medidas de la superficies, para poder trazar mapas topográficos que incluyan los accidentes naturales, para esto es necesario definir puntos coordenados orográficos de la zona, por tal complejidad de cálculos Gauss seria el encargado de dirigir el proyecto.
Durante el dominio francés ya se había hecho algún trabajo relacionado, sin embargo no había sido lo suficientemente preciso por lo que al final se decidió hacer la cartografía de nuevo. Para esta tarea Gauss inventó un instrumento llamado heliotropo con el cual se alineaban los instrumentos topográficos, este instrumento perduro por mucho tiempo, por su gran eficacia para hacer mediciones incluso en condiciones atmosféricas complicadas, otra cuestión que surgió durante este proyecto, fué la necesidad de adaptar la geometría plana a superficies esféricas problema resuelto por Gauss que dio origen a la denominada trigonometría esférica.

Como resultado de este nuevo proyecto Gauss regreso al tema de la Geometría, donde la solución de diversas problemáticas ocasionaron el planteamiento de las bases de la Geometría no Euclidiana y la Geometría Diferencial que llevaron a publicar su libro ” Disquisiciones Generales sobre Superficies Curvas “ surgida de sus observaciones sobre superficies geodésicas.
Este trabajo encuentra una aplicación practica muy clara en nuestra época, desde la perspectiva de la Geometría Euclidiana, la distancia mas corta entre dos puntos es una línea recta sin embargo, que pasa cuando un avión viaja de un punto a otro, en una supuesta línea recta, aquí es donde el trabajo de Gauss sobre geometría no euclidiana encuentra su aplicación mas evidente, en este ejemplo al viajar por el planeta no se describe una línea recta sino una una línea curva por lo cual, Se establece que la línea mas corta entre dos puntos sobre una superficie en este caso semejante a una esfera, es la línea Geodésica, un concepto novedoso propuesto en su libro sobre ” Geometría diferencial “, algunos matemáticos describen a “Disquisiciones Generales sobre Superficies Curvas ” como el trabajo mas perfecto en la carrera de Gauss.
“La Teoría General de la Relatividad”, nombre designado a la teoría gravitatoria publicada por Albert Einstein en 1915, donde establece que la fuerza de la gravedad es una manifestación local de la geometría del espacio-tiempo, tal geometría al no ser de tipo Euclídea impide construir este modelo relativista en ella , Sin embargo el matemático Georg Friedrich Bernhard Riemann, desarrolló parte las herramientas generales de la geometría no euclidiana en su tesis doctoral dirigida por Gauss, una de las herramientas matemáticas con las cuales Einstein construyó sus trabajos y su teoría mas famosa. En opinión de Einstein “La teoría de la relatividad no existiría sin la Geometría de Gauss”
Carl Friderich Gauss el Hombre.
Para el final de su vida Gauss, había pasado de ser el humilde hijo de granjeros a disponer de una fortuna mediana fruto de su trabajo, los últimos años los pasó ya como miembro de la burguesía. De ideología política conservadora sin embargo no se oponía a las reformas que fuesen debidamente justificadas.
En el ámbito religioso no era considerado ateo, aceptaba la existencia de Dios a través de la razón, su creencia se basaba en la armonía e integridad del gran diseño de la creación, pudiese ser considerada su visión de la religiosidad dentro de la postura filosófica del deísmo, creía en la inmortalidad del alma, pero no en el sentido de los postulados del cristianismo, siendo hasta contrario a las ideas de la Iglesia protestante Alemana.
Como persona a pesar de lo que se pudiese suponer, no era un antisocial retraído ajeno a la vida social, si no todo lo opuesto era un gran amante de la literatura inglesa apasionado de las novelas históricas de sir Walter Scott, extremadamente culto, dominó varios idiomas siendo esta actividad algo lúdico, creía que el aprender nuevos idiomas mantenía su mente joven y sana, quedan testimonios de que a los 68 años decidió aprender ruso sin ayuda de nadie, a los dos años ya leía obras en ruso con facilidad y escribía cartas a sus amigos científicos de San Petersburgo y en opinión de sus colegas rusos lo hablaba perfectamente.
Era un interesado del acontecer social del mundo, visitaba las bibliotecas con regularidad para mantenerse al tanto de los sucesos mundiales, leía los periódicos Internacionales y locales ya que le gustaba estar informado.
Las conquistas a la manera del Imperio napoleónico le parecían una incompresible locura guardándole cierto rechazo a todo lo francés derivado de los violentos acontecimientos de estos sobre su país. Su mayor ambición era el progreso de la matemáticas.

Medalla Premio Gauss 
Billete con la Imagen de Gauss
Siendo el 23 de Febrero de 1855 a la edad de 77 años murió a causa de complicaciones causadas por un padecimiento llamado hidropesía. El mismísimo rey de Hannover propuso en su honor acuñar una moneda en la cual se le otorgó el título de “El Príncipe de los Matemáticos ” . En el 2002 se creó un premio con su nombre el cual se otorga cada cuatro años a trabajos matemáticos que contribuyan con aplicaciones significativas fuera de las matemáticas, el galardón consiste en 10,000 euros, Y una medalla con la representación de la órbita de Ceres y un cuadrado que simboliza el método de los mínimos cuadrados herramienta utilizada para determinar dicha órbita.
Finalmente Recomiendo esta película llamada “Midiendo el Mundo” donde explora algunos momentos de la vida de esta gran mente.
Te Puede Interesar:
THE BREAKTHROUGH PRIZE
“LOS OSCARES DE LA CIENCIA “
Autor @Pablo_31416
Fuentes Consultadas
Antonio Rufián Lizana , Gauss, Una Revolución en Teoría de Números
Wikipediahttps://es.wikipedia.org/
Canales Youtube: Derivando, Archimedes Tube, Numberphile
Imágenes : https://www.mathunion.org, wikipedia


