Índice del Contenido
Geometría Euclidea vs Geometría Fractal
Uno de los aprendizajes mas tempranos de nuestra vida esta relacionado con la geometría, al tener juegos donde el objetivo es introducir figuras en orificios con la misma forma, o reconocer figuras de triángulos, cuadrados, círculos, y darles un nombre, iniciamos nuestra interacción con el entorno. Posteriormente durante nuestra formación escolar, en alguna de las primeras materias, aprendemos sobre líneas, triángulos, circunferencias, elipses las propiedades de estas y sus representaciones en el plano.
Es tan importante esta geometría que le dedicamos gran parte de nuestra formación profesional para entenderla y no es para menos, si no fuera por esta, jamás habríamos podido construir rascacielos, mecanismos para mover el mundo y fabricar todo tipo de herramientas, de ahí la importancia de capacitarnos para poder interactuar con nuestro mundo moderno.


Esta geometría Clásica creada por Euclides al rededor del siglo III a.C. con la que la humanidad ha construido el mundo moderno, ha permeado tan profundo en nuestra cultura y además está, tan sólidamente fundamentada que nos ha segado casi por completo.
Impidiendonos apreciar la geometría que está afuera de líneas rectas, rectángulos, triángulos etc. Al vivir en ciudades conformadas en su mayoría por figuras a partir de la geometría clásica, nos hemos creando un hábitat completamente artificial del cual es difícil que escape nuestra percepción enjaulada en este marco geométrico. Sin embargo fuera de está isla geométrica en la que vivimos, existe todo un océano irregular y caótico que obedece a sus propias reglas, a este océano llamado Geometría Fractal le dedicamos este artículo.

La Geometría de la Naturaleza.
Para poder salirnos de esa caja Euclidiana en la que nuestra mente vive, necesitamos hacer un ejercicio de observación a la mera usanza de la antigüedad. Basta con observar cuidadosamente un elemento del entorno cuyo origen sea natural, por ejemplo una roca, una rama de árbol o un brócoli y hacernos algunas preguntas ¿ Cuál es su forma? ¿Cómo están construidos ?, ¿Cuál es su estructura ? y tal vez después de reflexionar, nuestra mente finalmente……………………………………………….. se abra a este apasionante mundo infinito que nos rodea.



Que hace a un Fractal un Fractal.
Es algo complejo de definir, incluso en la actualidad existen diferentes formas de abordar, lo que es y no es un fractal, sin embargo nos inclinaremos a nombrar las características que la mayoría de estudiosos de la materia, concuerda para definiros. Al observar una montaña y una piedra podemos ver que la diferencia en su estructura es casi nula es decir si fuéramos un gigante y tomáramos la montaña en nuestra mano luciría como una piedra más, y si invertimos el ejercicio y nos hiciéramos diminutos la piedra luciría como una montaña.

¿Aun no queda claro ??? esta vez tomemos la rama de un árbol, y observemos las bifurcaciones de esta a lo largo del tallo, si la comparamos con el tronco del árbol del cual proviene, veríamos que es una estructura muy similar solo que tal vez mas delgada y sin tantas derivaciones de ramas. Sigues sin captar la esencia del concepto ? tranquilo, entrarás en shock después de este, vamos con el brócoli, si cortamos un trozo respetando el tallo veras que no importa que tan pequeño es el trozo es una versión más pequeña del trozo más grande, obteniendo siempre la misma estructura.

En todos los casos, es como si la misma estructura se repitiera, solo que a diferentes escalas dentro del mismo objeto. Un objeto compuesto de si mismo?, pues así es !! a esto se le llama autosimilitud, y es la primera característica de un Fractal, la simpleza de este tipo de estructuras es fascinante, un diseño simple pero eficaz para generar estructuras más complejas. Posteriormente se encontraría que las estructuras fractales tienen tres grados de autosimilitud de las cuales hablaremos mas adelante.

En 1919 el matemático Alemán Felix Hausdorff estableció el concepto de dimensión, lo que posteriormente dio origen al método matemático de dimensionamiento generalizado de Hausdorff – Besicovitch para objetos fractales, con el cual se pueden clasificar estos, donde se encontró teóricamente para el caso del (Copo de Kotch) que su longitud no puede ser mayor a 1.6 veces, este análisis dio pie a una de las características más impresionantes y útiles de estas estructuras, la relacionada con su dimensión fractal. Y esto ¿ Como se traduce en términos de la naturaleza ? pues que las estructuras originadas en la naturaleza poseen detalle a cualquier escala, lo que conocemos por rugosidad en el mundo natural.
Y a causa de esta rugosidad infinita, se puede deducir otra de sus características, continuando con el ejemplo del copo de Kotch, si quisiéramos aplicarle el concepto de recta tangente a alguno de sus puntos que se encuentran en su perímetro, encontraríamos que no hay ninguna recta que se ajuste a la definición de recta tangente, es decir una recta que toque a la curva en un punto dado, sin cortarla, por lo tanto se puede inferir otra de sus características, que los fractales no son curvas diferenciables, cuestión que valida el estado de rugosidad antes mencionado en cuerpos naturales. Algo muy llamativo en cuestiones geométricas clásicas.
Te puede interesar:
AJEDREZ
“El Deporte Ciencia”
El Padre de la Geometría Fractal
El matemático y catedrático de la universidad de Yale Benoit Mandelbrot (1924-2010) mejor conocido como el padre de la Geometría Fractal dio más formalidad a este fenómeno, ya que previo a él, solo se conocían a estas figuras como curiosidades que no aportaban gran valor a la ciencia, además de ser él, quien en 1975 les dio el nombre de Fractales del latin fractus ( quebrado ) encontró su interés por esta geometría en su fijeza sobre varias formas en la naturaleza que no encajaban en ninguna de las formas geométricas establecidas, como las nubes, montañas, costas, cortezas de árboles, rayos. Por tal motivo definió al conjunto de formas, que generalmente son producidas por un proceso iterativo (por repetición) como Fractales.
Aplicaciones en la Ciencia
El estudio de estas formas en la naturaleza no quedo en meras curiosidades matemáticas su estudio repercutió en múltiples aplicaciones tecnológicas siendo una de las primeras, y la cual abrió el campo de la investigación en esta área. El estudio de perturbaciones en las comunicaciones, mientras Mandelbrot trabajaba en IBM identificó un patrón fractal de ruido en las líneas de transmisión de sistemas de comunicación digital, lo que dificultaba la comunicación. Al analizar este patrón, se encontró uno de los fractales mas recurrentes en la naturaleza, él conocido como Polvo de Cantor en honor al matemático Ludwig Philipp Cantor famoso por establecer las bases de la teoría de conjuntos quien en 1883, determino un conjunto de números a los cuales este fractal obedece, razón por la que se le dio tal nombre a dicho patrón.
Este subconjunto fractal de números reales consiste gráficamente hablando en una línea que se divide en 3 segmentos, se retira el segmento de en medio y quedan 2 segmentos se repite el procedimiento infinitamente.

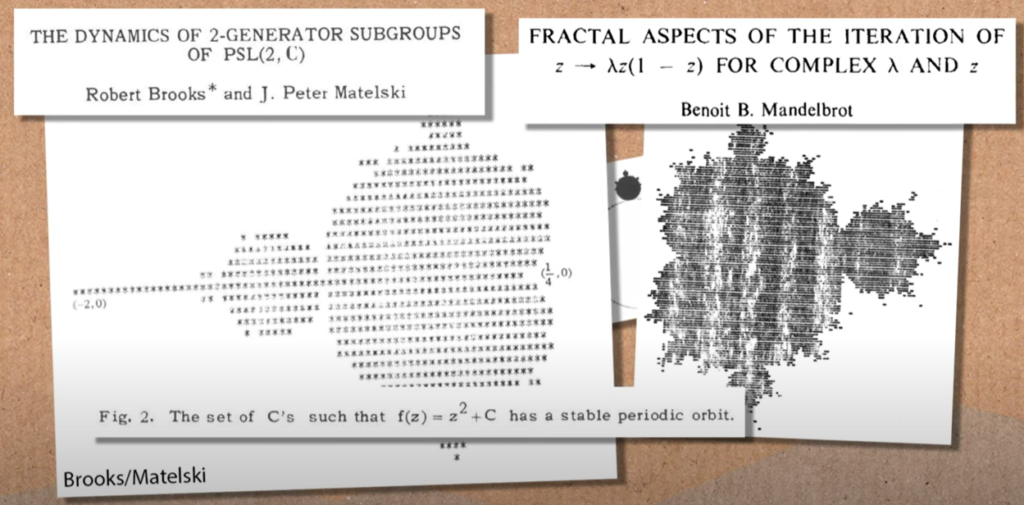
Conjunto de Mandelbrot
Uno de los trabajos pioneros en la construcción de conjuntos de números, basados en la repetición de operaciones fue el desarrollado por los franceses Gaston Julia y Pierre Fatou, Los cuales sirvieron como base para que a finales de los años setenta Mandelbrot se concentrara en estudiar esta área de las matemáticas, y como resultado construyó uno de los Fractales mas fascinantes y hermosos en el mundo de la geometría fractal, el popular Fractal de Mandelbrot.
Posteriormente los colores fueron agregados relacionando la periodicidad de las iteraciones (repeticiones) con respecto a una asignación de colores arbitraria. Pero mejor un vídeo para comprenderlo mejor.
Te puede Interesar:
NÚMEROS PRIMOS
” LOS NÚMEROS REBELDES “
Fractales más Populares!
La curva de Koch
Las Costas
Triangulo de Sierpinski
Alfombra de Sierpinski
Conjuntos de Julia
Fractal de Madelbrot
Curva de Hilbert
Influencian en la Cultura Popular
Pintura – La Gran Ola de Kanagawa.
Estampa Japonesa del artista Katsushika Hokusai publicada en 1830 forma parte de la serie treinta y seis vistas del monte Fuji. En esta se puede apreciar como las curvas mayores se originan en curvas menores representadas por pequeñas olas, asiendo alusión a una estructura fractal.

Arquitectura – El Lideta Mercado

Este centro comercial en la capital de Etiopía similar a una esponja de Menguer o cubo de Sierpinski , diseño que ayuda a proteger de las altas temperaturas y controla mejor la ventilación, inspirado en los diseños tradicionales encontrados en los tejidos de la cultura local.

Música Fractal
La música esta íntimamente relacionada con las matemáticas. Existen compositores que han encontrado en las estructuras generadas por fractales su inspiración para componer obras en los más diversos géneros desde música clásica, electrónica, ambiental, soundtracks para películas, etc. El compositor español y catedrático de la Academia de Bellas Artes de Granada, Francisco Guerrero Martín (1951-1997) desarrolló un método combinatorio fractal con el que en 1983 compuso su primera Obra Zayin I-VII, posteriormente también compondría música para largometrajes.
Escultura – Henry Segerman
El profesor investigador y artista matemático Henry Segerman, de la Universidad de Oklahoma, especialista en Topología Geométrica, se ha especializado en escultura a través de la impresión 3D. Autor del libro Visualizing Mathematics with 3D Printing, recrea modelos geométricos explorando las propiedades más fascinantes en la geometría, incluidas las estructuras fractales con lo que busca ejemplificar tangiblemente estas figuras, poniendo a disposición en su sitio web archivos descargables para su impresión en 3D.

Te puede Interesar:
GAUSS
” EL PRÍNCIPE DE LOS MATEMÁTICOS “
Pensamiento Fractal en la Inteligencia Artificial
El profesor Keith McGreggor del College of Computing at Georgia Tech, investigador del área Inteligencia Artificial y procesos cognitivos, en su conferencia TED expone sobre la forma en que el proceso de interpretación del mundo funciona entre los humanos y su entorno, como conseguimos distinguir elementos del entorno y como la visión moldea el pensamiento y viceversa, esto como preámbulo para técnicamente entender como podríamos crear un ente inteligente capaz de abstraer de lo que ve, información útil. Llegando a la hipótesis que para lograrlo es necesario tener la capacidad de distinguir dentro de patrones repetitivos naturales en el entorno, “la novedad” esa pequeña variación que se distingue dentro de un entorno cargado de información.
Poniendo aprueba esta idea en un programa computacional, experimenta el pensamiento fractal para resolver pruebas de forma más similar a la de los humanos teniendo excelentes resultados.
Construye tu Animación Fractal
Selecciona las figuras colores y dale en animar!!
Documental Completo – A la caza de la Dimensión Oculta.
Autor @Pablo_31416
Recursos Consultados
Libros: Vicente Talanquer, “Fractus, fracta, fractal: Fractales de Laberintos y Espejos”, Editorial Fondo de Cultura Económica.
Imagenes: Pixabay, wikipedia, GIPHY, Numberphile, Met Museum, Vilalta Studio,
Canales de Youtube: Acervo – Televisión Educativa, 3Blue1Brown, MITK12Videos, David programa, TED, Edumates
Paginas: Wikipedia, Centro de Documentación Musical de Andalucía, Henry’s Math(s) Website, College of Computing at Georgia Tech, sciencevsmagic.net
Mini Documental “Big Brains. Small Films. Benoît Mandelbrot, The Father of Fractals IBM”.