El decir que nuestra vida depende de los números primos sonaría un tanto exagerada, sin embargo, no está tan fuera de la realidad actual, tan es así que existe un tipo de regulación, que habla sobre números ilegales es decir cadenas de números que por su importancia en criptografía es ilegal poseerlos o distribuirlos por representar un peligro de seguridad y lo relacionado con la propiedad intelectual (copyright).
La importancia de los números primos, en esta nueva forma de sociedad es increíblemente grande, Pero … y ¿Cómo unos números pueden considerarse tan importantes? Hoy por hoy hemos construido como humanidad una nueva realidad, una realidad en la red, la cual ya es por lo menos hoy, igual de importante que la realidad fuera de ella, pasamos mucho tiempo en aplicaciones, servicios de streaming, hacemos transacciones de todo tipo, y todo esto basado en la confianza:
“Lo que ocurre dentro de la red, tiene una repercusión fuera de ella”
Esta confianza se ha ganado relativamente rápido gracias al respaldo de la seguridad o mejor dicho a la ciberseguridad.
Como quien pone un cerrojo en la puerta de su casa para no encontrar intrusos, La ciberseguridad es la llave y el candado del mundo virtual y aquí, es donde los números primos han encontrado una fuerte aplicación, si bien no son la única forma de generar ciberseguridad, si representan una de las formas más robustas de incrementar su efectividad haciéndola casi infalible.
Índice del Contenido
Qué son los Números Primos
Antes de dar una definición comprendamos que los números están agrupados en conjuntos. Estaremos trabajando en el conjunto de los números llamados Naturales que es donde se identifica este fenómeno numérico, De manera general y sin entrar en tantos detalles.
“Un Número Primo es Aquel que solo es Divisible por Sí mismo y por la Unidad “
Para dejarlo más claro veamos algunos Ejemplos de cómo se comportan los números que NO son primos también conocidos como números compuestos:
Digamos que quisiéramos generar el número 12:
- Podemos, generar el número 12 multiplicando un 6 por un 2: 6 x 2 = 12
- También podemos utilizar 4 multiplicado por 3: 4 x 3=12
- También podemos utilizar 2 por 2 por 3: 2 x 2 x 3=12
- Pero también 1 por 12: 1×12=12
Estos números que multiplicados dan como resultado el número que buscamos, se le llaman factores o divisores ya que todos estos factores dividen exactamente al número buscado, vemos otro Ejemplo:
Esta vez queremos generar el número 18:
- Podemos, generar el número 18 multiplicando un 6 por un 3: 6×3=18
- También podemos utilizar 9 multiplicado por 2: 9×2=18
- También podemos utilizar 3 por 3 por 2: 3x3x2=18
- Pero también 1 por 18: 1×18=18
Una vez más podemos observar que 18 tiene diferentes factores que pueden generarlo y cada uno lo divide de forma exacta.
Ahora veamos el caso de los números primos, repitiendo el ejercicio anterior Ejemplo:
Ahora queremos generar el número 13
- Veremos que la única forma de generarlo es tomando el 1 y multiplicarlo por el mismo 13 no hay otros factores para generarlo!
1×13=13
Ahora queremos generar el número 17
- La única forma de generarlo es tomando el 1 y multiplicarlo por el mismo 17 tampoco hay otros factores para generarlo!
1×17=17
Vayamos a uno más grande 23
- De nuevo solo lo podemos generar multiplicando 1 por 23 de igual manera no existen otros números para generarlo!!!!
1×23=23
Probemos con el 19
- También sólo podemos generarlo multiplicando 1 por 19 una vez más no existe otros factores para descomponer al 19
1×19=19
Con eso podemos entender mejor a que se refiere la regla de que solo son divisibles entre si mismo y la unidad!
Pero si regresamos al ejercicio anterior podemos ver que los números No primos pueden ser expresados en términos exclusivamente de números primos de lo cual podemos llegar a una primera conclusión al parecer todos los números compuestos pueden ser construidos exclusivamente por números primos, es como si estos fueran los ladrillos para poder construir a los demás números. Veamos la lista de los números primos encontrados del 1 al 100.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29,31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
Al observar esta pequeña lista aparentemente podemos observar algunas características, como que todos parecen ser impares a excepción del 2 o también que no aparentan tener un patrón definido, ni ser múltiplos entre ellos y si continuamos analizando más números siguen apareciendo.
Todas estas cuestiones han estado en la mente de los estudiosos de las matemáticas durante muchos años, se tienen registros de su estudio desde hace más de 2300 años, Son tan enigmáticos que se han convertido en casi una obsesión hasta nuestros días.
Podemos contar la historia de los números primos desde de los matemáticos que han buscado descifrarlos
Te Puede Interesar:
AJEDREZ
“El Deporte Ciencia “
Matemáticos vs Números Primos
La Aritmética rama de las matemáticas encargada del estudio, de todo lo relacionado con los números y las operaciones entre ellos, ha estudiado a los número primos, pero el interés en este tema no es nuevo.
La prueba más antigua sobre el interés de la humanidad en estos números data del año 6500 a.C. la cual es un hueso que fue encontrado en el norte de África en 1960, “El Hueso de Ishango” que tiene una serie de marcas estructuradas en columnas registrado los números 11, 13 , 17 y 19 que son los números primos comprendidos en el rango del 10 al 20 , también se pueden encontrar registros en la antigua china donde curiosamente se les dotaban de cualidades viriles, por no ser posible su descomposición en números menores.

Euclides 325-265 a. C.
Una de las mentes más brillantes el matemático Griego Euclides también conocido como “El padre de la Geometría” quien postulara una de las primeras demostraciones relacionada con los números primos lo que dio origen al llamado “El Teorema Fundamental de la Aritmética” que dice de forma general:
“Todo número natural se puede descomponer de forma única, como producto de factores primos”

Euclides llega a una de las primeras conclusiones, los números primos son infinitos, también define el concepto de máximo común divisor y mínimo común múltiplo, el cual se sigue utilizando actualmente para encontrar los factores de un número.
Eratóstenes de Cirene 273-194 a.C.
Eratóstenes matemático, astrónomo, y geógrafo Griego director de la mítica biblioteca de Alejandría, Conocido por ser uno de los primeros en calcular la circunferencia de la Tierra, creó uno de los métodos para identificar números primos llamado “La Criba de Eratóstenes” , la palabra Criba hace referencia a un utensilio en forma de malla que se utiliza para hacer una especie de filtrado (separación) de semillas o limpiar minerales, de ahí que el método de Eratóstenes criba los números naturales para dejar solo los números primos.
El método es el siguiente: Digamos que queremos cribar (separar) los números primos que hay entre el 1 y el 100, primero anotamos los números del 1 al 100 en una tabla.
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
Tomamos el primer número primo “2” y eliminamos a todos los múltiplos de éste y también el 1 q no es primo.
2 3 5 7 9 11 13
15 17 19 21 23 25 27
29 31 33 35 37 39 41
43 45 47 49 51 53 55
57 59 61 63 65 67 69
71 73 75 77 79 81 83
85 87 89 91 93 95 97
99
Tomamos el siguiente número primo el “3” y eliminamos a sus múltiplos
2 3 5 7 11 13
17 19 23 25 29 31
35 37 41 43 47 49
53 55 59 61 65 67
71 73 77 79 83 85
89 91 95 97
Tomamos el siguiente número primo el “5” y eliminamos a sus múltiplos
2 3 5 7 11 13
17 19 23 29 31 37
41 43 47 49 53 59
61 67 71 73 77 79
83 89 91 97
Tomamos el siguiente número primo el “7” y eliminamos a sus múltiplos
2 3 5 7 11 13
17 19 23 29 31 37
41 43 47 53 59 61
67 71 73 79 83 89
97
Podríamos continuar, con los siguientes números pero por inspección los números restantes no son múltiplos, así que son número primos:
2 3 5 7 11 13
17 19 23 29 31 37
41 43 47 53 59 61
67 71 73 79 83 89
97
Obsérvese que la criba finalizó al llegar a 10 que es la raíz de 100. De manera general, para encontrar todos los primos menores que un número N, basta con realizar la criba para los números menores o iguales a \sqrt{N} esto nos proporciona un límite para encontrar números menores que otro dado, este método se sigue utilizando, para encontrar números menores a diez mil millones.
Sin embargo la aparición de estos número es tan impredecible que por ejemplo entre 10^{100} y 10^1000 +1 solo hay 2 número primos, es sorprendente si se considera que son números de más de 100 cifras.
A partir de este método muchos estudiosos buscaron expresiones matemáticas para generar números primos, Aqui un video por si no quedó claro.
A partir del planteamiento de este método muchos matemáticos a lo largo de la historia han buscado una la expresión matemática general que de números primos, algunos de los matemáticos que han aportado con su genio son los siguientes.
Marin Mersenne 1588-1648
Filósofo, Matemático, Teólogo, Sacerdote de la Orden de los Mínimos (contradictoriamente a lo que se pudiese pensar, esta orden alentaba el saber científico y repudia el fanatismo ignorante ) fue el eje del movimiento intelectual europeo , defensor de pensamiento de Galileo, mantuvo una relación muy cercana con pensadores como René Descartes, Thomas Hobbes y Pierre Gassendí.
Este gran pensador encontró un comportamiento, que ha servido de pauta para su búsqueda que han utilizado posteriores matemáticos.

Mersenne afirmaba que todos los primos que hay entre 2 y 257, podían generarse con la expresión matemática siguiente:
2^p - 1
La cual suponía que daba como resultado un número primo siempre que p fuera alguno de los siguientes números:
Sin embargo por la complejidad de los cálculos no fue comprobada para todos los números “p” anteriores por Mersenne, posteriormente el matemático Leonhard Euler otra gran mente llegó a comprobar cien años después hasta p=31 es decir 2^{31}-1 y comprobó que era primo, algo que tiene una gran complejidad sin la ayuda de herramientas de cálculo modernas!!!! y hasta 1947 se encontró la lista completa al planteamiento de Marin Mersenne quedando:
p=2,3,5,7,13,17,19,
31,61,89,107,127
De modo que en la lista original, sobraban dos y faltaban tres números, la importancia de esta lista es muy grande, ya que en la actualidad las pruebas para saber si un número es primo (test de primalidad ) utiliza este conjunto de números. Hasta el año 2018, solo se han encontrado 51 números primos de Mersenne.
Pierre de Fermat 1601- 1665
En este camino por los números Primos llega una de las leyendas más impresionantes en el campo de la teoría de números. El autodenominado como: solo un aficionado a las matemáticas lo que le ganó el título de “El Príncipe de los Aficionados “.
Pierre de Fermat, Jurista (filósofo del derecho) de profesión, estudios que le permitieron ocupar un cargo de funcionario en la Consejería Real del Parlamento de Toulouse, dominaba las lenguas clásicas latín y griego, así como las lenguas europeas que se hablaban entonces, miembro de la alta sociedad, lo que le permitía dedicarse a su verdadera pasión los números, hizo múltiples aportaciones a diversas disciplinas matemáticas incluso postuló teoremas que fueron probados, apenas hace unos pocos años.

Esta inigualable mente propuso la siguiente expresión:
F_{n} = 2^{2^n} + 1
la cual es un método para saber si un número No es primo (también llamado número compuesto), sin la necesidad de encontrar ninguno de sus factores, esta aportación se enfoca en números muy grandes , además de conjeturar un conjunto de números los cuales se les conoce como los Números de Fermat.
Este teorema nunca fue demostrado por Fermat ya que consideraba que era muy largo, y el no era matemático, siendo demostrado por primera vez por Euler en 1736 y posteriormente por Gauss quedando registro en su libro Disquisitiones Arithmeticae publicado en 1801. Sin embargo Euler, encontró que la expresión no es válida al utilizar n=5 concluyendo que la Conjetura de Fermat era falsa, sin embargo esta propuesta de Fermat una vez más fué un paso adelante para ir entendiendo a estos números, además de sumar una herramienta, para confeccionar test de primalidad.
Leonhard Paul Euler 1707-1783
El matemático más prolífico de todos los tiempos, no existe rama de las matemáticas clásicas que este genio, no haya contribuido significativamente: Cálculo, Ecuaciones Diferenciales , Teoría de grafos, Geometría analítica, Teoría de números, etc. etc … También conocido por una de las constantes más utilizadas en la ciencia la cual lleva su nombre “e” la constante de Euler {\displaystyle{\text{e}}\ =2,718\;281\;828…}Introdujo la mayoría de la notación matemática que usamos actualmente, incluida la noción de función matemática.

De origen Suizo, se dice que una vez muerto se siguieron publicando trabajos suyos año tras año por la Academia de Ciencias de San Petersburgo Rusia, su obra ocupa, cerca de 90 volúmenes, Gran influencia sobre los posteriores genios matemáticos como Pierre Simon Laplace por tal motivo fue conocido como el “Maestro de todos Nosotros”
Euler mostró siempre gran interés sobre los números primos, construyendo tablas contenidos entre 1 y 100,000 esto lo llevó a formular expresiones matemáticas que los generaban, una de las más interesantes:
x^2+x+q
Dicha fórmula producía números primos para ciertos valores de x, como los comprendidos en q-2 tales como q=2,3,5,7,11,17
Christian Goldbach 1690-1764
Fue un Matemático Prusiano que tenía una estrecha relación con Euler, compartían por correspondencia sus hallazgos matemáticos y entre ellos ponían a prueba sus conjeturas, en una Carta recibida en 1952 por Euler, Goldbach afirmaba la siguiente proposición:
“Todo número par mayor que 2 puede escribirse como la suma de dos números primos, incluidos dos primos repetidos “

A finales de ese año Goldbach recibió la respuesta de Euler diciendo que había probado la conjetura hasta el número 1000, posteriormente en el año 1753 respondió que lo había probado hasta el número 2,500. Esta Conjetura ha sido comprobada por métodos informáticos para todos los números pares menores de dos mil billones. Como tal la conjetura no ha sido demostrada todavía y es considerada como uno de los problemas más difíciles de la historia.
Carl Friedrich Gauss 1777-1855
Nacido en Brunswick Alemania, de padres dedicados a las labores del campo, destinado a un futuro incierto, Se dio a notar en la escuela primaria a los nueve años resolviendo problemas matemáticos muy complejos para su edad, descubierto por su maestro como un niño especialmente dotado fue presentado al Conde de Brunswick el que se convertiría en su protector y lo alentaría para continuar sus estudios.
Se forjó una carrera profesional llegando a obtener el título de Catedrático de Astronomía y Director del observatorio Astronómico de la universidad de Gotinga. Apodado por sus colegas como “El príncipe de los Matemáticos”

Te Puede Interesar:
GAUSS
” EL PRÍNCIPE DE LOS MATEMÁTICOS “
Sin embargo al ser un genio del pensamiento divergente, es decir siempre abordando los problemas desde otra perspectiva, utilizó este talento para enfrentar el problema de los números primos, a diferencia de sus antecesores el no se enfocó en encontrar una fórmula matemática generadora de números primos, en vez de eso busco cuántos números primos existen entre dos números dados, es decir cuántos números hay entre 1 y 10 , 10 y 100 , 100 y 1000 etc. el buscaba estimar con qué frecuencia estos aparecían.
Para expresar esta relación Gauss definió la siguiente función (cabe mencionar que solo usa a pi como símbolo, no lo utiliza como la popular constante):
\pi(x) = Cantidad de Números primos menores que x
Por ejemplo se puede observar que entre los diez primeros números existen 4 números primos \pi(10)=4:
por lo tanto si se tiene una proporción \frac{4}{10}=0.4 obtenemos en este rango que el 40% son números primos y el 60% son números compuestos.
Otro ejemplo es que hasta 100 existen 25 números primos \pi(100)=25:
Se tendría la proporción de \frac{25}{100}=.25 se tiene un 25% de números primos y el 75% de números compuestos.
Donde se observa como la proporción de números primos va disminuyendo conforme se avanza a los números más grandes, por lo tanto es lógico pensar que los números primos vayan escaseando cada vez más, posteriormente utilizando logaritmos y diferentes cálculos basados en el razonamiento anterior formuló la siguiente expresión:
\cfrac{\pi(x)}{x}\thickapprox \cfrac{1}{ln x}
la cual da una estimación de la frecuencia con la que aparecen los números primos en una sucesión de números naturales la cual quedaría formalizada cien años después como el “Teorema de los Números Primos” uno de los más importantes en la historia de las matemática relacionado con los números primos.
Bernhard Riemann 1826-1866
Nacido en Bresselenz Alemania el extremadamente tímido Bernhard creció en una familia dedicada a la religión ya que su padre era un pastor Luterano, destinado a seguir sus pasos en la predicación, inició sus estudios en teología a los 19 años para complacer a su padre.
Desde pequeño demostró una gran habilidad de cálculo y por cuestiones fortuitas del destino, se cruzaron en su vida libros como la Teoría de Números del gran matemático francés Adrien-Marie Legendre además de presenciar conferencias impartidas por otro gran matemático Moritz Abraham Stern, algo que lo hizo inclinarse hacia las matemáticas, su tesis doctoral fue supervisada por Gauss. Bernhard Riemann transformó las matemáticas llevándolas hacia lugares jamás imaginados.

Riemann planteó uno de los aportes más grandes con respecto a los números primos lo relacionado a su distribución, conocida como la Hipótesis de Riemannn que valiéndose de la conjetura \pi(x) de Gauss y la función z de Euler amplio dicha función al capo de los números complejos. Con lo que obtuvo una imagen tridimensional de los ceros de la función z que representaba montañas y valles distribuidos con cierta regularidad llegando a enunciar:
“La parte real de todo cero no trivial de la función z es \cfrac{1}{2} “
Lo que significaría de ser cierta, que todos los números primos se distribuyen de una forma más regular de lo que se pensaba.
Srinivasa Ramanujan 1887-1920
Sin lugar a dudas uno de los matemáticos más enigmáticos de la historia de la humanidad, nacido en condiciones de extrema pobreza, en una pequeña comunidad llamada Erode en India, profesaba una forma de vida llamada Brahmin considerada una de las disciplinas de la más alta espiritualidad.
Este matemático autodidacta, con escasa formación académica, hizo aportaciones sumamente extraordinarias, llevó a cabo sus propias investigaciones carentes de la formalidad científica, pero con una profundidad reflexiva, que lo llevaron a las mismas conclusiones de matemáticos de gran renombre como el mencionado anteriormente Riemann, reunió en su corta vida 3900 resultados de forma independiente a todo el saber que se tenía en aquella época, la gran mayoría han sido validados. Lo más sorprendente es que él, argumentaba que estas construcciones matemáticas se le revelaban en sueños por la deidad familiar “Namagiri”.
La fecha de su nacimiento fue declarado como el día nacional de las matemáticas en India.

Encontró en el profesor Godfrey Harold Hard de la Universidad de Cambridge la oportunidad para que su genio fuera reconocido y así poder publicar su trabajo.
Sus aportaciones relacionada a los números primos son similares a las conseguidas por Riemann, a lo que Ramanujan Sostenía que tenía una fórmula para generar números primos con mayor exactitud, pero esto todavía es un debate entre los que analizan sus cuadernos de anotaciones.
Te Puede Interesar:
TÉCNICAS DE ESTUDIO
” Estudié y Reprobé !! Por qué? “
Minando Números Primos en la Actualidad
Como pudimos observar los personajes antes mencionados utilizaban el poder de la lógica matemática y diferentes aproximaciones para proponer y demostrar sus planteamientos, pero al tener números tan grandes cada vez, se volvía impráctico poder calcularlos.
Pudiéramos creer que en la actualidad utilizando herramientas computacionales acabaríamos con el enigma de los números primos, sin embargo todo lo contrario !! el uso de computadoras dedicadas a estos gigantescos cálculos, han generado otros problemas como el comprobar si los supuestos números primos realmente lo son, lo que lleva a diseñar test o pruebas de primalidad.
Un test de primalidad es un algoritmo que, dado un número de entrada n, no consigue verificar la hipótesis de que n es compuesto, estas pruebas son igual o más demandantes como la búsqueda de los mismo números, lo que significa una gran demanda de recursos de procesamiento, tiempo, energéticos, y económicos, pero en la actualidad se ha encontrado una forma colectiva de abordar este problema.
El Misterioso Proyecto GIMPS
¿Como se busca número primos en la actualidad aprovechando a las computadoras? una de las propuestas que ha dado grandes resultados, ha sido el proyecto llamado GIMP – ( Great Internet Mersenne Prime Search ) La Gran Búsqueda de Primos de Mersenne coordinada por Internet, la cual recurre al cómputo distribuido, bajo la filosofía de divide y vencerás, hace uso de miles de voluntarios a lo largo del mundo los cuales bajan el software Prime95, desde el cual se dividen los cálculos entre los equipos de cómputo de los voluntarios creando una de las más potentes redes de procesamiento distribuido del mundo este proyecto inició en 1997 y ha encontrado al menos los 13 últimos primos más grandes.
Este proyecto colectivo dio el 7 de Diciembre de, 2018 uno de los resultados más sorprendentes!!, el número primo más largo que se ha encontrado, Jonathan Pace ingeniero eléctrico estadounidense, encontró (su computadora procesó) el Primo de Mersenne, Nombrado como M(82 589 933) que cuenta con 23,249,425 digitos, pero para poder tener una mejor idea del tamaño de dicho primo este video se muestra dicho número impreso en su totalidad, abarcando 3 tomos.
Lo interesantes es que cualquiera puede participar en la búsqueda, simplemente hay q descargar el software hacer algunas configuraciones, además para la computadora que encuentre un número, hay una recompensa monetaria, pero sin duda lo más atractivo es ser parte de la pequeña lista de descubridores de números primos.
¿Y para que nos sirven?
Aparte de ser la base de las matemáticas y formar parte elemental de los sistemas de conteo, y el gran interés teórico que representan, aunado que a lo largo de su búsqueda han ocasionado el nacimiento de herramientas de cálculo imprescindibles para la informática, y como si esto no fuera lo suficientemente impresionante, se han encontrado en los átomos un comportamiento que se asemeja al comportamiento de los números primos vinculando las matemáticas a la física nuclear.
Pero hay un campo donde se ve claramente su utilidad práctica actual y es el de la criptografía, la cual nos sirve actualmente para mantener seguras diversas aplicaciones como, los correos electrónicos, las aplicaciones móviles, transacciones bancarias, tarjetas de crédito, comunicaciones por teléfonos móviles, etc. todas estas utilizan de alguna manera los números primos pero como es que funciona esto.

Números Primos y Criptografía
Aquí es donde los números primos cobran una importancia más allá de la mera teoría matemática y entran en nuestra vida cotidiana. En 1975 en la Universidad de Stanford W. Diffie y M. Hellman, desarrollaron el concepto de cifrado asimétrico también conocido como de clave pública, este concepto dio lugar a lo que posteriormente los científicos del MIT (Instituto Tecnológico de Massachusetts) Rivest, Shamir y Adleman crearán el sistema criptográfico de clave pública llamado RSA, sistema que ha cobrado notoriedad actual, al ser mencionado por plataformas de mensajería, pero y cuál es el papel de los números primos en este algoritmo de cifrado en este video podemos observar cómo funciona.
Con esto queda claro su uso práctico en las comunicaciones y que si en algún momento, se lograra descifrar el comportamiento los números primos, los sistemas criptográficos basados en estos se verían comprometidos. Por otro lado los sistemas criptográficos han evolucionado y existen otras variedades de algoritmos de cifrado, los cuales han mejorado y añadido más capas de seguridad, así que podemos estar tranquilos por el momento.
Los Números Prohibidos
A pesar de lo inverosímil que pueda sonar que existan números ilegales, ya no es tan descabellado después de lo descrito anteriormente. Si partimos de que los números primos son llaves criptográficas para abrir cerrojos virtuales que resguardan todo tipo de propiedades intangibles, pero sumamente importantes, desde conversaciones personales, e-mails, audios, videos, fotografías, acceso a cuentas de bancos, acceso a sistemas de seguridad y resguardo de propiedad intelectual.
Precisamente esta última fue una de las razones para la creación de una de las legislaciones que en 1999 la Digital Millennium Copyright Act estableció que se restringe el uso, almacenamiento, y distribución de números primos, que por sus características pudieran comprometer la seguridad nacional de dicho país o la propiedad intelectual de hardware y software, además de hacer énfasis en que cualquier forma de intervención (hackeo) encaminado en burlar la seguridad de DVDs y CDs ya sea por medio de software o hardware sería penado por esta ley, esto como una forma de reducir la piratería.
Otro ejemplo de números ilegales es el caso del PlayStation 3 en 2010 , esta popular consola de videojuegos se jactaba de ser la consola más segura en aquel momento hasta que el popular hacker Francis George Hotz mejor conocido como geohot y un grupo , de hackers llamado fail0verflowa aprovecharon algunas vulnerabilidades del hardware lo que los llevó a obtener la llave privada que les permitió modificar el sistema operativo, dándoles el control casi total de la consola.
Dicha llave privada servía como semilla, para generar un número aleatorio, esa llave privada es un número ilegal, y el que lograran obtenerla fue considerado un error crítico por Sony, el hackeo y la publicación de dicha llave le ganó graves problemas legales George Hotz, sin embargo es un gran ejemplo de lo peligrosos que pueden ser ciertas secuencias de números, ¿Que ocurriría si se obtuvieron las llaves privadas de por ejemplo un sistema financiero ?.
Te Puede Interesar:
FRACTALES
” LA GEOMETRÍA DE LA NATURALEZA “
Curiosidades
Algunos números primos poseen ciertas características que resultan curiosas, pero quien sabe tal vez en el futuro estas representen algún punto de partida para generar algún nuevo teorema
Números Capicúa
El número 313 es un número que puede leerse igual al derecho y al revés, de este tipo existen muchos en el universo numérico sin embargo el 313 es primo y capicua, además de si se escribe en código binario 100111001 continúa siendo primo y es el único número primo de tres dígitos que tiene esta propiedad.
Otro ejemplo de número capicúa más grande es el:
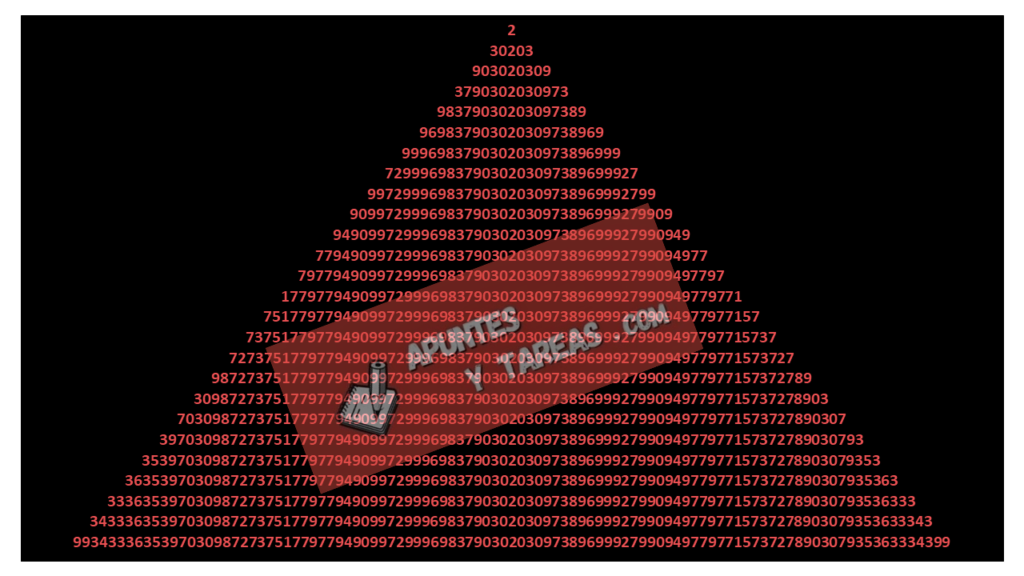
99343336353970309872737517797794909972999698379030203097389699927990949779771573727890307935363334399
Con nada más y nada menos que 101 cifras, puede ser leído por igual de inicio a fin y viceversa quedando el mismo número, y si tienen muuchoo! tiempo pueden comprobar que es primo, además si vas eliminando los dos primeros números y los dos últimos, se respeta que siga siendo capicúa y primo, y dichos resultados pueden formar una pirámide finalizando en la punta con el número 2 que es primo !!
Los Repunit
Los llamados Números repunit o repituno abreviatura de repeated unit, acuñado en 1966 por Albert H. Beiler. son aquellas series de varios 1 como por ejemplo el repunit:
1111111111111111111
El cual está compuesto por 19 números uno, que por supuesto es primo, o por ejemplo el
11111111111111111111111
Que tiene 23 números 1 y es primo
Las Extrañas Series del 91
Uno de los números primos que encierra un comportamiento muy curioso es el 91 que está formado por sus factores primos 13 \cdot 7 = 91, lo interesante es cuando agregamos al final de dicho número una serie de ceros terminados en uno, resulta en una alternancia entre un número primo y un número compuesto (no primo ).
99901 primo
999001 compuesto
99990001 primo
99999000001 compuesto
999999000001 primo
99999990000001 compuesto
9999999900000001 primo
999999999000000001 compuesto
99999999990000000001 compuesto 🙁
Curiosamente la secuencia de alternancia se rompe justo después de rebasar las 9 repeticiones del número 9
Primos Gemelos
Los números primos gemelos son aquellos números primos que distan entre ellos de 2 unidades nombrados así por el matemático alemán Paul Stäckel.
Ejemplo:
3 y 5
11 y 13
17 y 19
y una larga lista:
(29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463), (521, 523), (569, 571), (599, 601), (617, 619), (641, 643), (659, 661), (809, 811), (821, 823), (827, 829), (857, 859), (881, 883).
El espiral de Números Primos
Otra de las curiosidades visualmente interesantes es la de graficar la distribución números primos en un sistema de coordenadas polares lo que genera un interesante patrón Espiral de Arquímedes
Te Puede Interesar:
THE BREAKTHROUGH PRIZE
“ LOS OSCARES DE LA CIENCIA “
Autor @Pablo_31416
Fuentes Consultadas:
Textos: Gracián Enrique 2010 Los Números Primos “Un Largo Camino al Infinito”
Páginas: wikipedia.org, mersenne.org/
Canales Youtube: Numberphile, Derivando, Archimedes Tube, Modern Vintage Gamer,BBC News Mundo,TED-Ed
Imágenes: Pixabay, Wikipedia, Giphy,